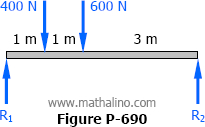
Solution to Problem 696-697 | Beam Deflection by Method of Superposition
Problem 696
In Fig. P-696, determine the value of P for which the deflection under P will be zero.
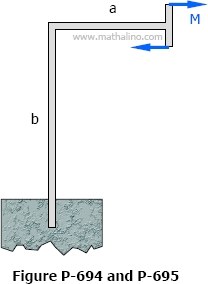
Solution to Problem 694-695 | Beam Deflection by Method of Superposition
Problem 694
The frame shown in Fig. P-694 is of constant cross section and is perfectly restrained at its lower end. Compute the vertical deflection caused by the couple M.
Solution to Problem 693 | Beam Deflection by Method of Superposition
Problem 693
Determine the value of EIδ at the left end of the overhanging beam in Fig. P-693.
Solution to Problem 692 | Beam Deflection by Method of Superposition
Problem 692
Find the value of EIδ midway between the supports for the beam shown in Fig. P-692. (Hint: Combine Case No. 11 and one half of Case No. 8.)
Solution to Problem 691 | Beam Deflection by Method of Superposition
Problem 691
Determine the midspan deflection for the beam shown in Fig. P-691. (Hint: Apply Case No. 7 and integrate.)
Solution to Problem 689 | Beam Deflection by Method of Superposition
Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 106 psi.
Solution to Problem 688 | Beam Deflection by Method of Superposition
Problem 688
Determine the midspan value of EIδ at the left end of the beam shown in Fig. P-688.
Solution to Problem 687 | Beam Deflection by Method of Superposition
Problem 687
Determine the midspan deflection of the beam shown in Fig. P-687 if E = 10 GPa and I = 20 × 106 mm4.
Solution to Problem 686 | Beam Deflection by Method of Superposition
Problem 686
Determine the value of EIδ under each concentrated load in Fig. P-686.