Problem 726 | Fully restrained beam with concentrated load at midspan
Problem 726
A beam of length L, perfectly restrained at both ends, supports a concentrated load P at midspan. Determine the end moment and maximum deflection.
concentrated load
Problem 710 | Two simple beams at 90 degree to each other
Problem 710
Two timber beams are mounted at right angles and in contact with each other at their midpoints. The upper beam A is 2 in wide by 4 in deep and simply supported on an 8-ft span; the lower beam B is 3 in wide by 8 in deep and simply supported on a 10-ft span. At their cross-over point, they jointly support a load P = 2000 lb. Determine the contact force between the beams.
Problem 656 | Beam Deflection by Conjugate Beam Method
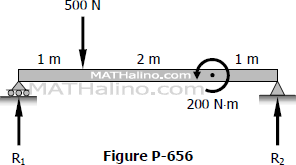
Problem 656
Find the value of EIδ at the point of application of the 200 N·m couple in Fig. P-656.
- Read more about Problem 656 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
Problem 655 | Beam Deflection by Conjugate Beam Method
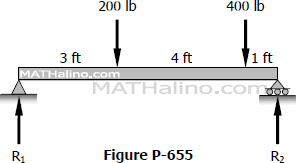
Problem 655
Find the value of EIδ under each concentrated load of the beam shown in Fig. P-655.
Solution to Problem 696-697 | Beam Deflection by Method of Superposition
Problem 696
In Fig. P-696, determine the value of P for which the deflection under P will be zero.
Solution to Problem 694-695 | Beam Deflection by Method of Superposition
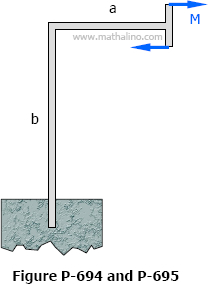
Problem 694
The frame shown in Fig. P-694 is of constant cross section and is perfectly restrained at its lower end. Compute the vertical deflection caused by the couple M.
Solution to Problem 693 | Beam Deflection by Method of Superposition
Problem 693
Determine the value of EIδ at the left end of the overhanging beam in Fig. P-693.
Solution to Problem 690 | Beam Deflection by Method of Superposition
Problem 690
The beam shown in Fig. P-690 has a rectangular cross section 50 mm wide. Determine the proper depth d of the beam if the midspan deflection of the beam is not to exceed 20 mm and the flexural stress is limited to 10 MPa. Use E = 10 GPa.
Solution to Problem 689 | Beam Deflection by Method of Superposition
Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 106 psi.
Solution to Problem 687 | Beam Deflection by Method of Superposition
Problem 687
Determine the midspan deflection of the beam shown in Fig. P-687 if E = 10 GPa and I = 20 × 106 mm4.