Let
x = length of side
DE
From right triangle CEB
$\sin 60^\circ = \dfrac{h}{12}$
$h = 12 \sin 60^\circ$
$h = 10.3923 \, \text{ cm}$
$\frac{1}{3}h = 3.4641 \, \text{ cm}$
Radius of the circle
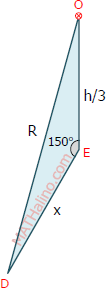$R = OB = \frac{2}{3}h$
$R = 6.9282 \, \text{ cm}$
Cosine law for triangle DEO
$R^2 = x^2 + (\frac{1}{3}h)^2 - 2x(\frac{1}{3}h) \cos 150^\circ$
$6.9282^2 = x^2 + 3.4641^2 - 2x(3.4641)(-0.866)$
$48 = x^2 + 12 + 6x$
$x^2 + 6x - 36 = 0$
$x = 3.7082 \, \text{ and } \, -9.7082 \, \text{ (absurd)}$
$x = 3.7082 \, \text{ cm}$ answer
