Problem 328 | Equilibrium of Force System

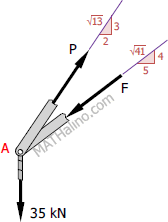
$\Sigma F_H = 0$

$F(\frac{5}{\sqrt{41}}) = P(\frac{2}{\sqrt{13}})$

$F = 0.7104P$
 

$\Sigma F_V = 0$

$P(\frac{3}{\sqrt{13}}) = F(\frac{4}{\sqrt{41}}) + 35$

$P(\frac{3}{\sqrt{13}}) = (0.7104P)(\frac{4}{\sqrt{41}}) + 35$

$0.3883P = 35$

$P = 90.14 \, \text{ kN}$           answer
 

$F = 0.7104(90.14)$

$F = 64.03 \, \text{ kN}$           answer