Problem 327 | Equilibrium of Force System

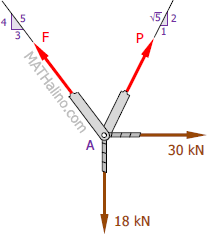
$\Sigma F_H = 0$

$F(\frac{3}{5}) = P(\frac{1}{\sqrt{5}}) + 30$

$F = \frac{\sqrt{5}}{3}P + 50$       →   Equation (1)
 

$\Sigma F_V = 0$

$P(\frac{2}{\sqrt{5}}) + F(\frac{4}{5}) = 18$

$\frac{\sqrt{5}}{2}P + F = 22.5$
 

Substitute F of Equation (1)
$\frac{\sqrt{5}}{2}P + (\frac{\sqrt{5}}{3}P + 50) = 22.5$

$\frac{5\sqrt{5}}{6}P = -27.5$

$P = -14.76 \, \text{ kN}$           answer
 

From Equation (1)
$F = \frac{\sqrt{5}}{3}(-14.76) + 50$

$F = 39 \, \text{ kN}$           answer