Problem 269 | Resultant of Non-Concurrent Force System

Let F₄ = the fourth force
 

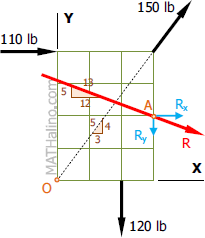$R_x = 390(\frac{12}{13})$

$R_x = 360 \, \text{ lb to the right}$
 

$\Sigma F_x = R_x$

$110 + 150(\frac{3}{5}) + F_{4x} = 360$

$F_{4x} = 160 \, \text{ lb to the right}$
 

$R_y = 390(\frac{5}{13})$

$R_y = 150 \, \text{ lb downward}$
 

$\Sigma F_y = R_y$

$-150(\frac{4}{5}) + 120 + F_{4y} = 150$

$F_{4y} = 150 \, \text{ lb downward}$
 

$F_4 = \sqrt{{F_{4x}}^2 + {F_{4y}}^2}$

$F_4 = \sqrt{160^2 + 150^2}$

$F_4 = 219.32 \, \text{ lb}$
 

$\tan \theta_x = \dfrac{F_{4y}}{F_{4x}}$

$\tan \theta_x = \dfrac{150}{160}$

$\theta_x = 43.15^\circ$
 

$M_O = 2R_x + 3R_y$

$M_O = 2(360) + 3(150)$

$M_O = 1170 \, \text{ lb}\cdot\text{ft clockwise}$
 

Resolve F₄ into components at the x-axis
$\Sigma Fd = M_O$

$110(4) + 120(2) + F_{4y}i_x = 1170$

$110(4) + 120(2) + 150i_x = 1170$

$i_x = 3.27 \, \text{ ft to the right of O}$
 

Resolve F4 into components at the y-axis
$\Sigma Fd = M_O$

$110(4) + 120(2) + F_{4x}i_y = 1170$

$110(4) + 120(2) + 160i_y = 1170$

$i_y = 3.06 \, \text{ ft above point O}$
 

Thus, F₄ = 219.32 lb downward to the right at θ_x = 43.15° with x-intercept i_x = 3.27 to the right of O, and y-intercept i_y = 3.06 ft above point O.