Clock-related Problems
There are 12 dial units in the clock. Every time the minute hand completes 12 dials, the hour hand moves 1 dial. Thus, if the minute hand moves by x the hour hand moves by x/12.
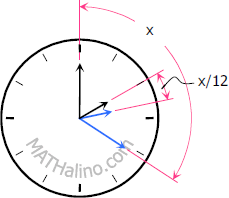
Key equations:
$\dfrac{x}{12}$ = distance traveled by the hour hand (in minutes)
There are three common questions in clock problems; (1) time when the hands of the clock are together, (2) time when the hands of the clock are perpendicular to each other, and (3) time when the hands of the clock form a straight line.
The following are the distances between the hands of the clock:
(1) Together = 0
(2) Perpendicular (90° to each other) = 15 minutes
(3) Straight line (opposite each other) = 30 minutes
The table below is provided for the sake of completeness of this post.
| Dial position | No. of minutes |
| 12:00 | 0 minute |
| 1:00 | 5 minutes |
| 2:00 | 10 minutes |
| 3:00 | 15 minutes |
| 4:00 | 20 minutes |
| 5:00 | 25 minutes |
| 6:00 | 30 minutes |
| 7:00 | 35 minutes |
| 8:00 | 40 minutes |
| 9:00 | 45 minutes |
| 10:00 | 50 minutes |
| 11:00 | 55 minutes |
| 12:00 | 60 minutes |
- Log in to post comments
