Working Stress Design of Reinforced Concrete

Back to top

Working Stress Design

Working Stress Design is called Alternate Design Method by NSCP (National Structural Code of the Philippines) and ACI (American Concrete Institute, ACI).
 

Code Reference
NSCP 2010, Section 424: Alternate Design Method
ACI 318M-99, Appendix A: Alternate Design Method

 

Back to top

Notation

f_c = allowable compressive stress of concrete
f_s = allowable tesnile stress of steel reinforcement
f'_c = specified compressive strength of concrete
f_y = specified yield strength of steel reinforcement
E_c = modulus of elasticity of concrete
E_s = modulus of elasticity of steel
n = modular ratio
M = design moment
d = distance from extreme concrete fiber to centroid of steel reinforcement
kd = distance from the neutral axis to the extreme fiber of concrete
jd = distance between compressive force C and tensile force T
ρ = ratio of the area of steel to the effective area of concrete
β_c = ratio of long side to short side of concentrated load or reaction area
A_s = area of steel reinforcement

 

Back to top

Design Principle

The design concept of WSD is based on Elastic Theory in which the stress-strain diagram is within the proportional limit and will obey Hooke's Law.
 

Actual Stress ≤ Allowable Stress

 

Back to top

Allowable Stresses

(NSCP 2010, 424.4.1 / ACI 318M, A.3.1)

Concrete

1.	Flexure
	Extreme fiber stress in compression	$0.45f'_c$
2.	Shear
	Beams and one-way slabs and footings:
	Shear carried by concrete, $v_c$	$0.09\sqrt{f'_c}$
	Maximum shear carried by concrete plus shear reinforcement, $v_c$	$0.38\sqrt{f'_c}$
	Joists:
	Shear carried by concrete, $v_c$	$0.09\sqrt{f'_c}$
	Two-way slabs and footings:
	Shear carried by concrete, $v_c$ but not greater than $\frac{1}{6}\sqrt{f'_c}$	$\frac{1}{12}(1 + 2/\beta_c)\sqrt{f'_c}$
3.	Bearing on loaded area	$0.3f'_c$

 

Steel Reinforcement

1.	Grade 275 or Grade 350 reinforcement	140 MPa
2.	Grade 420 reinforcement or greater and welded wire fabric (plain or deformed)	170 MPa
3.	For flexural reinforcement, 10 mm or less in diameter, in one-way slabs of not more than 4 m span but not greater than 200 MPa	0.50fy

 

Back to top

Modulus of Elasticity

Modulus of Elasticity of Concrete (NSCP 408.6.1)
For weight of concrete, w_c between 1500 and 2500 kg/m³
$E_c = {w_c}^{1.5}0.043\sqrt{f'_c}$
 

For normal weight concrete
$E_c = 4700\sqrt{f'_c}$
 

Modulus of Elasticity of Steel Reinforcement (NSCP 408.6.2)
For nonprestressed reinforcement
$E_s = 200\,000 ~ \text{MPa}$

 

Back to top

Modular Ratio

(NSCP 424.6.4) It shall be permitted to take the modular ratio, $n = \dfrac{E_s}{E_c}$ as the nearest whole number (but not less than 6).
 

Modular Ratio for Beams with Compression Steel (NSCP 424.6.5)
In doubly reinforced flexural members, an effective modular ratio of $2n$ shall be used to transform compression reinforcement for stress computations.

 

Back to top

Assumptions in WSD

1. Plane section remains plane before and after bending.
2. Concrete stress varies from zero at the neutral axis to a maximum at the extreme fiber.
3. Concrete do not carry tensile stress. All tensile stress will be carried by steel reinforcement.
4. The steel and concrete are perfectly bond so that no slippage between the two will occur.

 

 

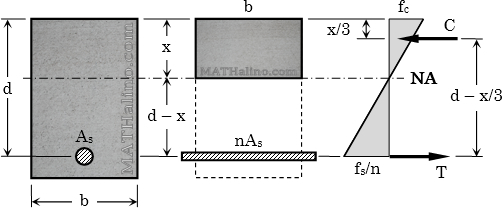
Moment of area:
$Q_{\text{above NA}} = Q_{\text{below NA}}$

$\frac{1}{2}bx^2 = nA_s(d - x)$
 

Tensile and Compressive Forces
$T = f_s A_s$

$C = \frac{1}{2}f_c bx$

$C = T$
 

Moment in the section
$y = d - \frac{1}{3}x$

$M = Cy$

$M = Ty$
 

Bending stresses
$I_{NA} = \dfrac{bx^3}{3} + nA_s(d - x)^2$

$f_c = \dfrac{Mx}{I_{NA}}$

$\dfrac{f_s}{n} = \dfrac{M(d - x)}{I_{NA}}$