WSD Method
Example 01: Total Compression Force at the Section of Concrete Beam
Problem
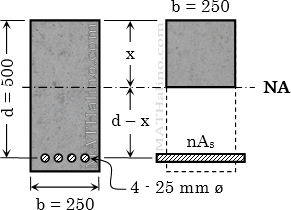
A rectangular reinforced concrete beam with width of 250 mm and effective depth of 500 mm is subjected to 150 kN·m bending moment. The beam is reinforced with 4 – 25 mm ø bars. Use alternate design method and modular ratio n = 9.
- What is the maximum stress of concrete?
- What is the maximum stress of steel?
- What is the total compressive force in concrete?
Example 01: Required Steel Area of Reinforced Concrete Beam
Problem
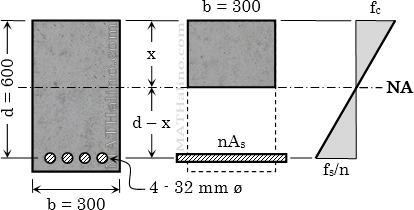
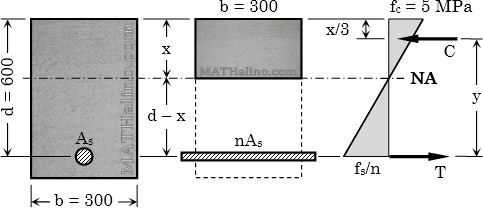
A rectangular concrete beam is reinforced in tension only. The width is 300 mm and the effective depth is 600 mm. The beam carries a moment of 80 kN·m which causes a stress of 5 MPa in the extreme compression fiber of concrete. Use n = 9.
1. What is the distance of the neutral axis from the top of the beam?
2. Calculate the required area for steel reinforcement.
3. Find the stress developed in the steel.
Working Stress Design of Reinforced Concrete
Working Stress Design is called Alternate Design Method by NSCP (National Structural Code of the Philippines) and ACI (American Concrete Institute, ACI).
Code Reference
NSCP 2010 - Section 424: Alternate Design Method
ACI 318 - Appendix A: Alternate Design Method
Notation
fs = allowable tesnile stress of steel reinforcement
f'c = specified compressive strength of concrete
fy = specified yield strength of steel reinforcement
Ec = modulus of elasticity of concrete
Es = modulus of elasticity of steel
n = modular ratio
M = design moment
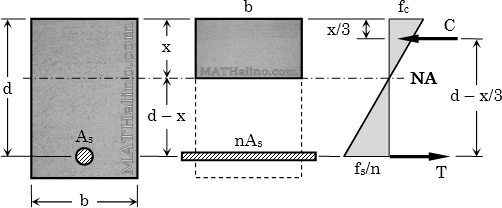
d = distance from extreme concrete fiber to centroid of steel reinforcement
kd = distance from the neutral axis to the extreme fiber of concrete
jd = distance between compressive force C and tensile force T
ρ = ratio of the area of steel to the effective area of concrete
As = area of steel reinforcement
- Read more about Working Stress Design of Reinforced Concrete
- Log in to post comments