Active forum topics
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Application of Differential Equation: Newton's Law of Cooling
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
- Eliminate the Arbitrary Constants
- Law of cosines
- Maxima and minima (trapezoidal gutter)
- Special products and factoring
New forum topics
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
- Integration of 4x^2/csc^3x√sinxcosx dx
- Maxima and minima (trapezoidal gutter)
- Special products and factoring
- Newton's Law of Cooling
- Find the roots of the quadratic equation by differentiation method
Recent comments
- Bakit po nagmultiply ng 3/4…4 weeks 1 day ago
- Determine the least depth…10 months 3 weeks ago
- Solve mo ang h manually…4 weeks 1 day ago
- Paano kinuha yung height na…11 months 1 week ago
- It's the unit conversion…11 months 2 weeks ago
- Refer to the figure below…11 months 1 week ago
- where do you get the sqrt414 weeks 1 day ago
- Thank you so much4 weeks 1 day ago
- How did you get the 2.8 mins…4 weeks 1 day ago
- How did you get the distance…4 weeks 1 day ago

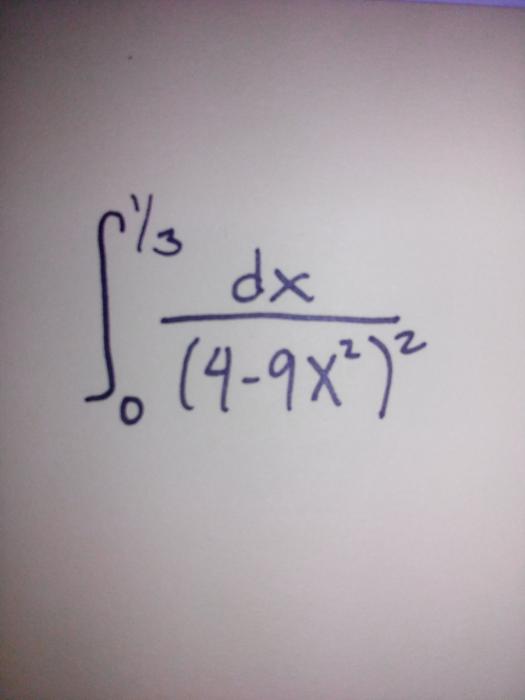

Re: definite integral hirap po talaga hindi ko masagot
$\displaystyle \int_0^{1/3} \dfrac{dx}{(4 - 9x^2)^2}$
$\displaystyle = \int_0^{1/3} \dfrac{dx}{[ \, 2^2 - (3x)^2 \, ]^2}$
Let
3x = 2 sin θ
3 dx = 2 cos θ dθ
dx = (2/3) cos θ dθ
When
x = 0, θ = 0,
x = 1/3, θ = 30° = π/6
Hence,
$\displaystyle \int_0^{1/3} \dfrac{dx}{(4 - 9x^2)^2}$
$\displaystyle = \int_0^{\pi/6} \dfrac{\frac{2}{3} \cos \theta \, d\theta}{[ \, 2^2 - (2\sin \theta)^2 \, ]^2}$
$\displaystyle = \dfrac{1}{24} \int_0^{\pi/6} \dfrac{\cos \theta \, d\theta}{(1 - \sin^2 \theta)^2}$
$\displaystyle = \dfrac{1}{24} \int_0^{\pi/6} \dfrac{\cos \theta \, d\theta}{\cos^4 \theta}$
$\displaystyle = \dfrac{1}{24} \int_0^{\pi/6} \dfrac{d\theta}{\cos^3 \theta}$
$\displaystyle = \dfrac{1}{24} \int_0^{\pi/6} \sec^3 \theta \, d\theta$
For
Let
u = sec θ
du = sec θ tan θ dθ
dv = sec2 θ dθ
v = tan θ
$\displaystyle \int \sec^3 \theta \, d\theta$
$\displaystyle = \sec \theta \, \tan \theta - \int \tan \theta (\sec \theta \, \tan \theta) \, d\theta$
$\displaystyle = \sec \theta \, \tan \theta - \int \tan^2 \theta \sec \theta \, d\theta$
$\displaystyle = \sec \theta \, \tan \theta - \int (\sec^2 \theta - 1) \sec \theta \, d\theta$
$\displaystyle = \sec \theta \, \tan \theta - \int \sec^3 \theta \, d\theta + \int \sec \theta \, d\theta$
$\displaystyle 2\int \sec^3 \theta \, d\theta = \sec \theta \, \tan \theta + \int \sec \theta \, d\theta$
$\displaystyle 2\int \sec^3 \theta \, d\theta = \sec \theta \, \tan \theta + \ln (\sec \theta + \tan \theta)$
$\displaystyle \int \sec^3 \theta \, d\theta = \frac{1}{2}\sec \theta \, \tan \theta + \frac{1}{2}\ln (\sec \theta + \tan \theta)$
Hence,
$\displaystyle \int_0^{1/3} \dfrac{dx}{(4 - 9x^2)^2}$
$\displaystyle = \dfrac{1}{24} \int_0^{\pi/6} \sec^3 \theta \, d\theta$
$= \dfrac{1}{24} \left[ \dfrac{1}{2}\sec \theta \, \tan \theta + \dfrac{1}{2}\ln (\sec \theta + \tan \theta) \right]_0^{\pi/6}$
$= \dfrac{1}{48} \left[ \sec \theta \, \tan \theta + \ln (\sec \theta + \tan \theta) \right]_0^{\pi/6}$
$= \dfrac{1}{48} \left[ \sec \dfrac{\pi}{6} \, \tan \dfrac{\pi}{6} + \ln \left( \sec \dfrac{\pi}{6} + \tan \dfrac{\pi}{6} \right) \right] \\ ~ ~ ~ ~ ~ - \dfrac{1}{48} \left[ \sec 0 \, \tan 0 + \ln \left (\sec 0 + \tan 0 \right) \right]$
$= \dfrac{1}{48} \left[ \dfrac{2}{\sqrt{3}} \left( \dfrac{\sqrt{3}}{3} \right) + \ln \left( \dfrac{2}{\sqrt{3}} + \dfrac{\sqrt{3}}{3} \right) \right] - \dfrac{1}{48} \left[ 1(0) + \ln \left( 1 + 0 \right) \right]$
$= \dfrac{1}{48} \left[ \dfrac{2}{3} + \ln \left( \sqrt{3} \right) \right]$
$= 0.0253$
Re: definite integral hirap po talaga hindi ko masagot
In reply to Re: definite integral hirap po talaga hindi ko masagot by Jhun Vert
thank you po talaga.atsaka bakit po pala naging pie over 6?
Re: definite integral hirap po talaga hindi ko masagot
In reply to Re: definite integral hirap po talaga hindi ko masagot by Jeanvill Palad…
Multiply by π/180 to convert degree to radian:
$30^\circ = 30^\circ \times \dfrac{\pi}{180^\circ} = \dfrac{\pi}{6} ~ \text{rad}$
pwd muh rin e direct sa
pwd muh rin e direct sa calculator pra m check muh ang sagot muh pg tama