Solution to Problem 559 | Built-up Beams | Strength of Materials Review at MATHalino

Problem 559
A beam is composed of 6 planks, each 100 mm wide and 20 mm thick, piled loosely on each other to an overall dimension of 100 mm wide by 120 mm high. (a) Compare the strength of such a beam with that of a solid beam of equal overall dimensions. (b) What would be the ratio if the built-up beam consisted of a 12 planks each 100 mm wide by 10 mm thick?

Solution 559

Click here to expand or collapse this section

Part (a)

For 1 plank

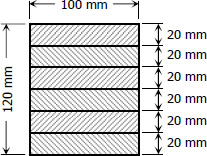$I_1 = \dfrac{100(20^3)}{12}$

$I_1 = \frac{200\,000}{3} \, \text{mm}^4$

For the whole beam
$I = 6I_1 = 6(200\,000/3)$

$I = 400\,000 \, \text{mm}^4$

$\dfrac{M}{EI} = \dfrac{M_1}{E_1 I_1}$ where E₁ = E

$\dfrac{M}{E(400\,000)} = \dfrac{M_1}{E(\frac{200\,000}{3})}$

$\dfrac{M_1}{M} = \dfrac{1}{6}$ answer

Part (b)

For 1 plank

$I_1 = \dfrac{100(10^3)}{12}$

$I_1 = \frac{25\,000}{3} \, \text{mm}^4$

For the whole beam
$I = 12I_1 = 12(25\,000/3)$

$I = 100\,000 \, \text{mm}^4$

$\dfrac{M}{EI} = \dfrac{M_1}{E_1 I_1}$ where E₁ = E

$\dfrac{M}{E(100\,000)} = \dfrac{M_1}{E(\frac{200\,000}{3})}$

$\dfrac{M_1}{M} = \dfrac{1}{12}$ ) answer

Tags

flexural stress

built-up beam

Aerisk16 Thu, 08/22/2024 - 01:08

I think what is ask is the comparison of the strength of the built-up beam consisting of 6 planks - 100 mm x 20 mm dimension, resulting in an overall dimensions of 100 mm X 120 mm to the strength of a solid beam with a dimension of 100mm x 120mm.. we compare the section modulus of the beams. The beam cross section with higher section modulus is stronger since it experiences less flexural stress (assuming built up beam and solid beam are subjected to the same loading (same bending moment)). I'm kind of like confuse with the solution above, comparing the strength of 1 plank to the strength of 6 planks combine...

Jhun Vert Thu, 08/22/2024 - 17:21

Yes you are absolutely right. We flagged this page for revision. Note that after revision is made, our comments will be put to archive. Thank you for calling our attention, highly appreciated.

Solution to Problem 559 | Built-up Beams

Navigation

Recent comments

I think what is ask is the…

Yes you are absolutely right…

Navigation

Recent comments