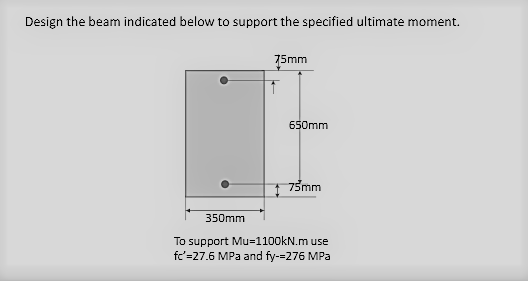
I need guidance in designing a beam supporting specified ultimate moment of 1100 kN.m (doubly reinforced beam)
- Log in to post comments
 MATHalinoEngineering Math Review
MATHalinoEngineering Math Review Forum posts (unless otherwise specified) licensed under a Creative Commons Licence.
Forum posts (unless otherwise specified) licensed under a Creative Commons Licence.
Given:
Given:
Mu = 1100 kN-m
f'c = 27.6 MPa
fy = 276 MPa
Step 1 - Calculate β1 and ρmax
β1 = 0.85
ρmax = β1 * 0.85 * f'c * 3/ fy * 7
ρmax = 0.85*0.85*276*3/ 276 * 7
ρmax = 0.030964
Step 2 - Calculate Rmax
Rmax = ρmax * fy *(1-ρmax* fy/1.7*f'c)
Rmax = 0.0300964* 276*(1-(0.00309*276/(1.7*27.6))
Rmax = 6.9895 MPa
Step 3 - Calculate Mmax and compare with Mu
Mmax = Rmax * φ * b * d^2
Mmax = 6.9895 * 0.90 * 350 * 725^2
Mmax = 1,157.265 kN-m
Mu = 1100 kN-m < Mmax = 1,157.626 kN-m
Hence, The beam can be designed as Singly-Reinforced Beam (SRB)