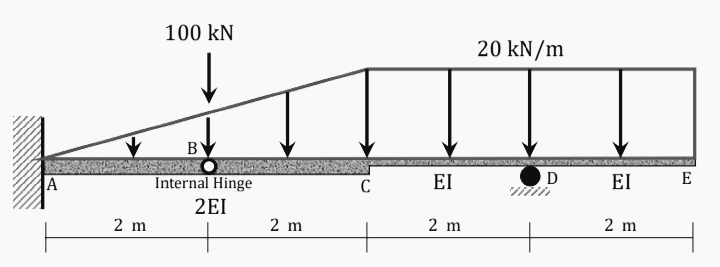
Theory of Structure: Area-Moment Method

Isolate the segments to the left of B and to the right of B, then solve for the reactions.
 

$M_A = -256.67 ~ \text{kN}\cdot\text{m}$

$R_A = 131.67 ~ \text{kN}$

$R_B = 21.67 ~ \text{kN}$

$R_D = 88.33 ~ \text{kN}$
 

Draw then the moment diagram by parts for each segment. Look for the best location of moment center for your diagram. I chose B for segment AB and C for segment BE. You may choose another point per your judgement.
 

Notice that the value of moments under segments containing 2EI are divided by 2.
 

Draw the approximate elastic curve (not shown) and based on your drawing proceed with the concepts of area moment method to solve for the required. I will show here the calculations for the deflection at B knowing that the tangent to the elastic curve at A is horizontal.
 

$\delta_B = \dfrac{1}{EI} \, t_{B/A}$

$\delta_B = \dfrac{1}{EI}\left( \text{Area}_{AB} \right) \cdot \bar{X_B}$
 

From the Moment Diagram by Parts
$\delta_B = \dfrac{1}{EI} \Big[ \frac{1}{2}(2)(131.67)\left( \frac{2}{3} \right) - 128.33(2)(1) - \frac{1}{4}(2)(3.33)\left( \frac{2}{5} \right) \Big]$

$\delta_B = -\dfrac{169.56}{EI} ~ \text{kN}\cdot\text{m}^3$
 

The negative sign in the answer indicates that B is below the tangent line through A which is our reference tangent for the deviation.
 

In the same way, analyze the tangents and the elastic curve to get the rest of the required items.
 

I request you share to us your solution when you're done.