Derivation of Formula for Radius of Circumcircle
The formula for the radius of the circle circumscribed about a triangle (circumcircle) is given by
where At is the area of the inscribed triangle.
Derivation of Formula for Radius of Incircle
The radius of incircle is given by the formula
where At = area of the triangle and s = semi-perimeter.
- Read more about Derivation of Formula for Radius of Incircle
- Log in to post comments
Derivation of Cosine Law
The following are the formulas for cosine law for any triangles with sides a, b, c and angles A, B, C, respectively.
$b^2 = a^2 + c^2 - 2ac\cos B$
$c^2 = a^2 + b^2 - 2ab\cos C$
- Read more about Derivation of Cosine Law
- Log in to post comments
Derivation of Sine Law
For any triangles with vertex angles and corresponding opposite sides are A, B, C and a, b, c, respectively, the sine law is given by the formula...
- Read more about Derivation of Sine Law
- Log in to post comments
Derivation of Sum and Difference of Two Angles
 The sum and difference of two angles can be derived from the figure shown below.
The sum and difference of two angles can be derived from the figure shown below.
- Read more about Derivation of Sum and Difference of Two Angles
- Log in to post comments
Derivation of Formula for Sum of Years Digit Method (SYD)
The depreciation charge and the total depreciation at any time m using the sum-of-the-years-digit method is given by the following formulas:
Depreciation Charge:
Total depreciation at any time m
Where:
FC = first cost
SV = salvage value
n = economic life (in years)
m = any time before n (in years)
SYD = sum of years digit = 1 + 2 + ... + n = n(1 + n)/2
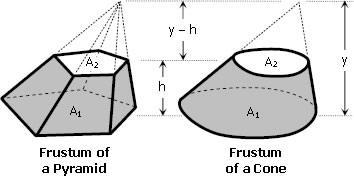
Derivation of formula for volume of a frustum of pyramid/cone
Frustum of a pyramid and frustum of a cone
The formula for frustum of a pyramid or frustum of a cone is given by
Where:
h = perpendicular distance between A1 and A2 (h is called the altitude of the frustum)
A1 = area of the lower base
A2 = area of the upper base
Note that A1 and A2 are parallel to each other.
Solution to Problem 341 | Torsion of thin-walled tube
Problem 341
Derive the torsion formula τ = Tρ / J for a solid circular section by assuming the section is composed of a series of concentric thin circular tubes. Assume that the shearing stress at any point is proportional to its radial distance.
Derivation of the Double Angle Formulas
The Double Angle Formulas can be derived from Sum of Two Angles listed below:
$\sin (A + B) = \sin A \, \cos B + \cos A \, \sin B$ → Equation (1)
$\cos (A + B) = \cos A \, \cos B - \sin A \, \sin B$ → Equation (2)
$\tan (A + B) = \dfrac{\tan A + \tan B}{1 - \tan A \, \tan B}$ → Equation (3)
- Read more about Derivation of the Double Angle Formulas
- Log in to post comments
Relationship Between Arithmetic Mean, Harmonic Mean, and Geometric Mean of Two Numbers
For two numbers x and y, let x, a, y be a sequence of three numbers. If x, a, y is an arithmetic progression then 'a' is called arithmetic mean. If x, a, y is a geometric progression then 'a' is called geometric mean. If x, a, y form a harmonic progression then 'a' is called harmonic mean.
Let AM = arithmetic mean, GM = geometric mean, and HM = harmonic mean. The relationship between the three is given by the formula
Below is the derivation of this relationship.