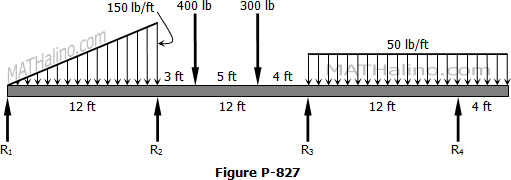
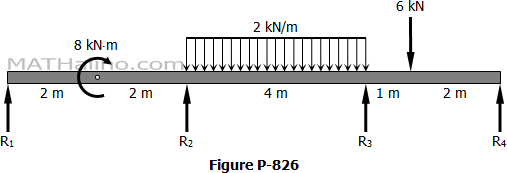
Continuous Beam With Equal Support Reactions
Situation
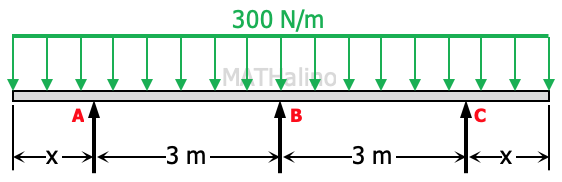
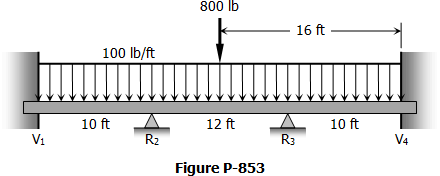
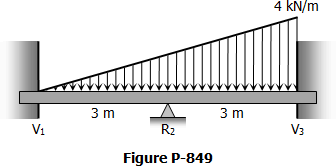
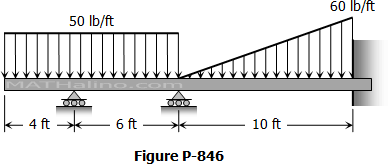
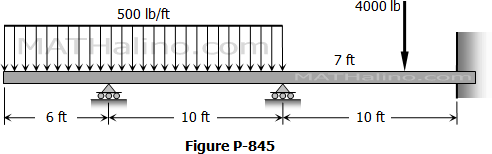
A beam 100 mm × 150 mm carrying a uniformly distributed load of 300 N/m rests on three supports spaced 3 m apart as shown below. The length x is so calculated in order that the reactions at all supports shall be the same.
1. Find x in meters.
| A. 1.319 | C. 1.217 |
| B. 1.139 | D. 1.127 |
2. Find the moment at B in N·m.
| A. -240 | C. -242 |
| B. -207 | D. -226 |
3. Calculate the reactions in Newton.
| A. 843.4 | C. 863.8 |
| B. 425.4 | D. 827.8 |
- Read more about Continuous Beam With Equal Support Reactions
- Log in to post comments