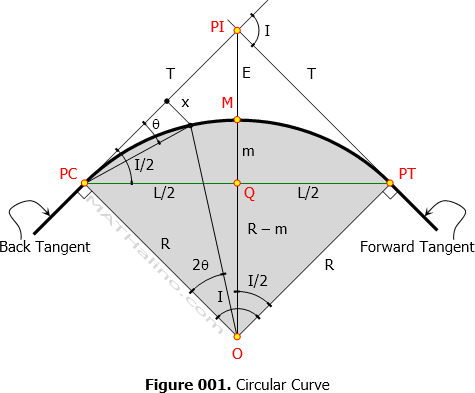
Simple Curves
Terminologies in Simple Curve
- PC = Point of curvature. It is the beginning of curve.
- PT = Point of tangency. It is the end of curve.
- PI = Point of intersection of the tangents. Also called vertex
- T = Length of tangent from PC to PI and from PI to PT. It is known as subtangent.
- R = Radius of simple curve, or simply radius.
- L = Length of chord from PC to PT. Point Q as shown below is the midpoint of L.
- Lc = Length of curve from PC to PT. Point M in the the figure is the midpoint of Lc.
- E = External distance, the nearest distance from PI to the curve.
- m = Middle ordinate, the distance from midpoint of curve to midpoint of chord.
- I = Deflection angle (also called angle of intersection and central angle). It is the angle of intersection of the tangents. The angle subtended by PC and PT at O is also equal to I, where O is the center of the circular curve from the above figure.
- x = offset distance from tangent to the curve. Note: x is perpendicular to T.
- θ = offset angle subtended at PC between PI and any point in the curve
- D = Degree of curve. It is the central angle subtended by a length of curve equal to one station. In English system, one station is equal to 100 ft and in SI, one station is equal to 20 m.
- Sub chord = chord distance between two adjacent full stations.
Sharpness of circular curve
The smaller is the degree of curve, the flatter is the curve and vice versa. The sharpness of simple curve is also determined by radius R. Large radius are flat whereas small radius are sharp.
Formulas for Circular Curves
The formulas we are about to present need not be memorized. All we need is geometry plus names of all elements in simple curve. Note that we are only dealing with circular arc, it is in our great advantage if we deal it at geometry level rather than memorize these formulas.
Length of tangent, T
Length of tangent (also referred to as subtangent) is the distance from PC to PI. It is the same distance from PI to PT. From the right triangle PI-PT-O,
$\tan \dfrac{I}{2} = \dfrac{T}{R}$
External distance, E
External distance is the distance from PI to the midpoint of the curve. From the same right triangle PI-PT-O,
$\cos \dfrac{I}{2} = \dfrac{R}{R + E}$
$R + E = \dfrac{R}{\cos \dfrac{I}{2}}$
Middle ordinate, m
Middle ordinate is the distance from the midpoint of the curve to the midpoint of the chord. From right triangle O-Q-PT,
$\cos \dfrac{I}{2} = \dfrac{R - m}{R}$
$R \cos \dfrac{I}{2} = R - m$
Length of long chord, L
Length of long chord or simply length of chord is the distance from PC to PT. Again, from right triangle O-Q-PT,
$\sin \dfrac{I}{2} = \dfrac{L/2}{R}$
$R \sin \dfrac{I}{2} = L/2$
Length of curve, Lc
Length of curve from PC to PT is the road distance between ends of the simple curve. By ratio and proportion,
$\dfrac{L_c}{I} = \dfrac{2\pi R}{360^\circ}$
An alternate formula for the length of curve is by ratio and proportion with its degree of curve.
$\dfrac{L_c}{I} = \dfrac{1 \, station}{D}$
$L_c = \dfrac{1 \, station \times I}{D}$
English system: 1 station = 100 ft
If given the stationing of PC and PT
Degree of curve, D
The degree of curve is the central angle subtended by an arc (arc basis) or chord (chord basis) of one station. It will define the sharpness of the curve. In English system, 1 station is equal to 100 ft. In SI, 1 station is equal to 20 m. It is important to note that 100 ft is equal to 30.48 m not 20 m.
In arc definition, the degree of curve is the central angle angle subtended by one station of circular arc. This definition is used in highways. Using ratio and proportion,
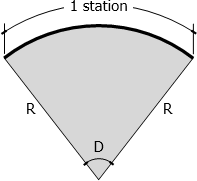
$\dfrac{1 \, station}{D} = \dfrac{2\pi R}{360^\circ}$
English system (1 station = 100 ft):
Chord Basis
Chord definition is used in railway design. The degree of curve is the central angle subtended by one station length of chord. From the dotted right triangle below,
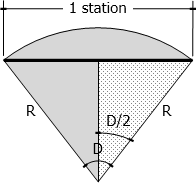
$\sin \dfrac{D}{2} = \dfrac{half \,\, station}{R}$
English system (half station = 50 ft):
Back to top
Minimum Radius of Curvature
Vehicle traveling on a horizontal curve may either skid or overturn off the road due to centrifugal force. Side friction f and superelevation e are the factors that will stabilize this force. The superelevation e = tan θ and the friction factor f = tan ϕ. The minimum radius of curve so that the vehicle can round the curve without skidding is determined as follows.
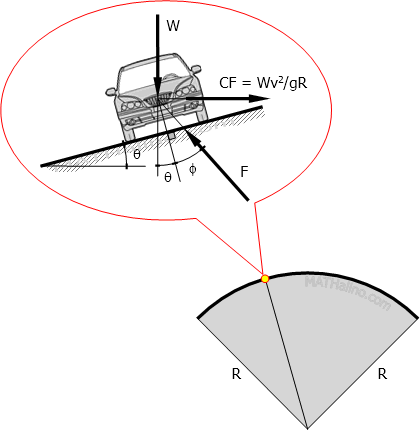
From the force polygon shown in the right
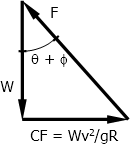 $\tan (\theta + \phi) = \dfrac{CF}{W}$
$\tan (\theta + \phi) = \dfrac{CF}{W}$
$\tan (\theta + \phi) = \dfrac{\dfrac{Wv^2}{gR}}{W}$
$\tan (\theta + \phi) = \dfrac{Wv^2}{WgR}$
$\tan (\theta + \phi) = \dfrac{v^2}{gR}$
The quantity v2/gR is called impact factor.
Impact factor
Back to the equation tan (θ + ϕ) = v2/gR
$\tan (\theta + \phi) = \dfrac{v^2}{gR}$
$\dfrac{\tan \theta + \tan \phi}{1 - \tan \theta \, \tan \phi} = \dfrac{v^2}{gR}$
Recall that $\tan \theta = e$ and $\tan \phi = f$
$\dfrac{e + f}{1 - ef} = \dfrac{v^2}{gR}$
But $ef \equiv 0$, thus
$e + f = \dfrac{v^2}{gR}$
Radius of curvature with R in meter and v in meter per second
For the above formula, v must be in meter per second (m/s) and R in meter (m). For v in kilometer per hour (kph) and R in meter, the following convenient formula is being used.
$R = \dfrac{\left( v \dfrac{\text{km}}{\text{hr}} \right)^2 \left( \dfrac{1000 \, \text{m}}{\text{km}} \times \dfrac{1 \, \text{ hr}}{3600 \text{ sec}} \right)^2}{g(e + f)}$
$R = \dfrac{v^2 \left( \dfrac{1}{3.6}\right)^2}{g(e + f)}$
$R = \dfrac{v^2}{(3.6^2)g(e + f)}$
$R = \dfrac{v^2}{(3.6^2)(9.80)(e + f)}$
Radius of curvature with R in meter and v in kilometer per hour
Using the above formula, R must be in meter (m) and v in kilometer per hour (kph).
