Compound and Reversed Curves

Back to top

Compound Curves

A compound curve consists of two (or more) circular curves between two main tangents joined at point of compound curve (PCC). Curve at PC is designated as 1 (R₁, L₁, T₁, etc) and curve at PT is designated as 2 (R₂, L₂, T₂, etc).
 

 

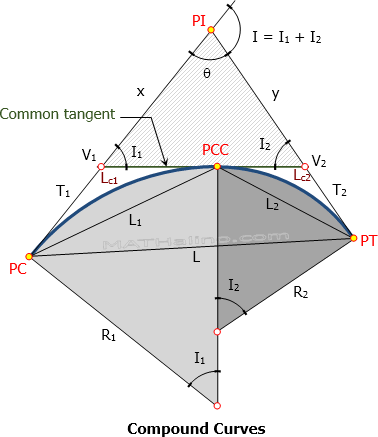
Elements of compound curve

• PC = point of curvature
• PT = point of tangency
• PI = point of intersection
• PCC = point of compound curve
• T₁ = length of tangent of the first curve
• T₂ = length of tangent of the second curve
• V₁ = vertex of the first curve
• V₂ = vertex of the second curve
• I₁ = central angle of the first curve
• I₂ = central angle of the second curve
• I = angle of intersection = I₁ + I₂
• L_c1 = length of first curve
• L_c2 = length of second curve
• L₁ = length of first chord
• L₂ = length of second chord
• L = length of long chord from PC to PT
• T₁ + T₂ = length of common tangent measured from V₁ to V₂
• θ = 180° - I
• x and y can be found from triangle V₁-V₂-PI.
• L can be found from triangle PC-PCC-PT

 

Finding the stationing of PT

Given the stationing of PC
$\text{Sta PT} = \text{Sta PC} + L_{c1} + L_{c2}$
 

Given the stationing of PI
$\text{Sta PT} = \text{Sta PI} - x - T_1 + L_{c1} + L_{c2}$

 

Back to top

Reversed Curve

Reversed curve, though pleasing to the eye, would bring discomfort to motorist running at design speed. The instant change in direction at the PRC brought some safety problems. Despite this fact, reversed curves are being used with great success on park roads, formal paths, waterway channels, and the like.
 

 

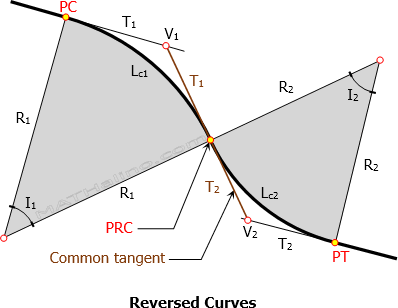
Elements of Reversed Curve

• PC = point of curvature
• PT = point of tangency
• PRC = point of reversed curvature
• T₁ = length of tangent of the first curve
• T₂ = length of tangent of the second curve
• V₁ = vertex of the first curve
• V₂ = vertex of the second curve
• I₁ = central angle of the first curve
• I₂ = central angle of the second curve
• L_c1 = length of first curve
• L_c2 = length of second curve
• L₁ = length of first chord
• L₂ = length of second chord
• T₁ + T₂ = length of common tangent measured from V₁ to V₂

 

Finding the stationing of PT

Given the stationing of PC
$\text{Sta PT} = \text{Sta PC} + L_{c1} + L_{c2}$

Given the stationing of V₁
$\text{Sta PT} = \text{Sta } V_1 - T_1 + L_{c1} + L_{c2}$

 

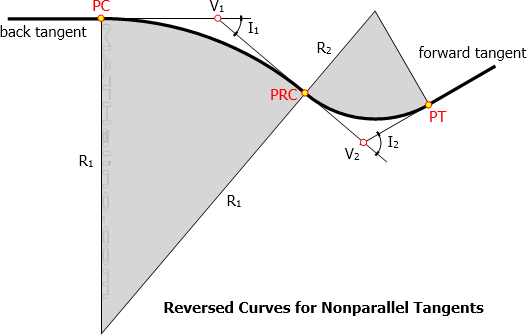
Reversed Curve for Nonparallel Tangents
The following figure is an example reversed curves of unequal radii connecting non-parallel tangents.
 

 

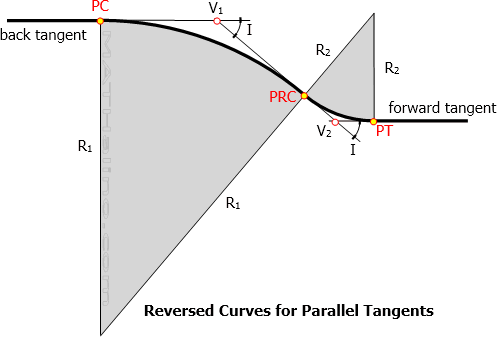
Reversed Curve for Parallel Tangents
The figure below is an example of reversed curves of unequal radii connecting two parallel roads.