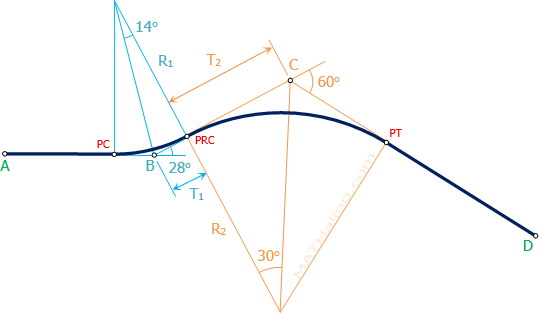
Reversed Curve to Connect Three Traversed Lines
Situation
A reversed curve with diverging tangent is to be designed to connect to three traversed lines for the portion of the proposed highway. The lines AB is 185 m, BC is 122.40 m, and CD is 285 m. The azimuth are Due East, 242°, and 302° respectively. The following are the cost index and specification:
Number of Lanes = Two Lanes
Width of Pavement = 3.05 m per lane
Thickness of Pavement = 280 mm
Unit Cost = P1,800 per square meter
It is necessary that the PRC (Point of Reversed Curvature) must be one-fourth the distance BC from B.
- Find the radius of the first curve.
A. 123 m
B. 156 m
C. 182 m
D. 143 m - Find the length of road from A to D. Use arc basis.
A. 552 m
B. 637 m
C. 574 m
D. 468 m - Find the cost of the concrete pavement from A to D.
A. P2.81M
B. P5.54M
C. P3.42M
D. P4.89M