radius of curvature
Curvature and Radius of Curvature
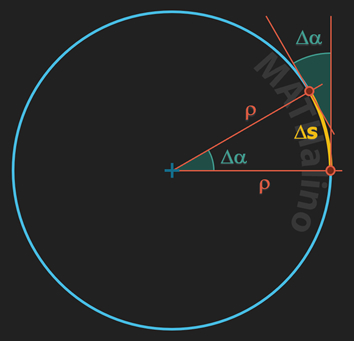
Curvature (symbol, $\kappa$) is the mathematical expression of how much a curve actually curved. It is the measure of the average change in direction of the curve per unit of arc. Imagine a particle to move along the circle from point 1 to point 2, the higher the number of $\kappa$, the more quickly the particle changes in direction. This quick change in direction is apparent in smaller circles.
- Read more about Curvature and Radius of Curvature
- Log in or register to post comments
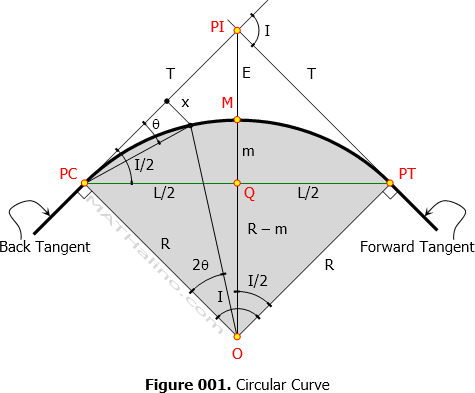
Simple Curves
Formulas for Circular Curves
The formulas we are about to present need not be memorized. All we need is geometry plus names of all elements in simple curve. Note that we are only dealing with circular arc, it is in our great advantage if we deal it at geometry level rather than memorize these formulas.
- Read more about Simple Curves
- Log in or register to post comments