Curvature and Radius of Curvature
Curvature (symbol, $\kappa$) is the mathematical expression of how much a curve actually curved. It is the measure of the average change in direction of the curve per unit of arc. Imagine a particle to move along the circle from point 1 to point 2, the higher the number of $\kappa$, the more quickly the particle changes in direction. This quick change in direction is apparent in smaller circles.
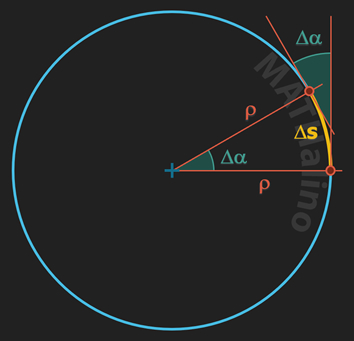
$\Delta s = \rho \cdot \Delta \alpha$
$\dfrac{1}{\rho} = \dfrac{\Delta \alpha}{\Delta s}$ ← the curvature
Let 1/ρ = κ
$\kappa = \dfrac{\Delta \alpha}{\Delta s}$
It is important to note that curvature κ is reciprocal to the radius of curvature ρ according to the above equations.
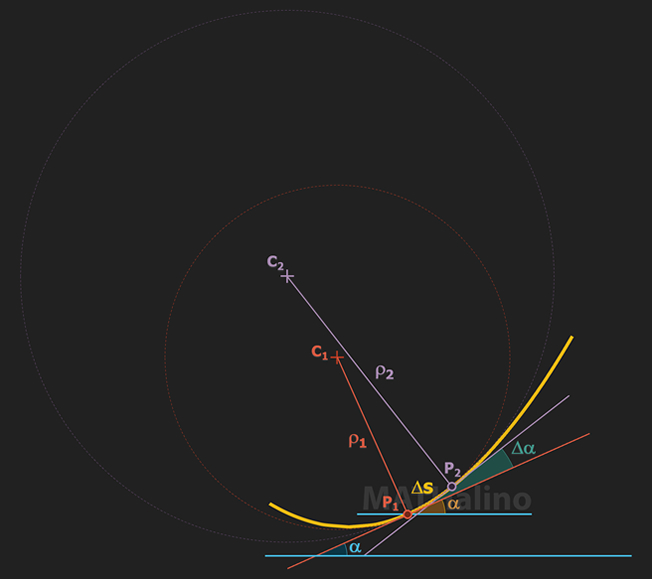
As P2 approaches P1, the ratio Δα/Δs approaches a limit. This limit is the curvature of the curve at a particular point, and from the above figure that point is P1.
$\displaystyle \kappa = \lim_{\Delta s \to 0}\dfrac{\Delta \alpha}{\Delta s}$
$\kappa = \dfrac{da}{ds}$
Curvature in xy-Plane
In a circle, κ is constant, however, if the curve in question is not a circle, κ represents the average curvature of the arc at a particular point.
From Analytic Geometry, the slope of the line m is equal to the tangent of angle of inclination, or m = tan α. Note that in Calculus, m = dy/dx.
$\tan \alpha = y'$
$\alpha = \arctan y'$
Differentiate both sides with respect to x:
$d\alpha = \dfrac{y'' \, dx}{1 + (y')^2}$
Note that the Differential Length of Arc in the xy-plane is given by this formula:
$ds = \sqrt{1 + (y')^2} \, dx$
Hence,
$\kappa = \dfrac{da}{ds} = \dfrac{\dfrac{y'' \, dx}{1 + (y')^2}}{\sqrt{1 + (y')^2} \, dx}$
Simplify the equation above, and we have this formula for Curvature:
And for the Radius of Curvature:
- Log in to post comments
