Solution to Problem 598 | Spacing of Rivets or Bolts in Built-Up Beams

From Illustrative Problem 591
τ = 100 MPa shear stress
σ_b = 220 MPa bearing stress for single shear rivet
σ_b = 280 MPa bearing stress for double shear rivet
 

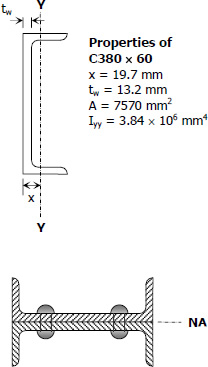By transfer formula for moment of inertia
$I = \bar{I} + Ad^2$

$I_{NA} = 2 \, [ \, (3.84 \times 10^6) + 7570(19.7^2) \, ]$

$I_{NA} = 13\,555\,682.6 \, \text{ mm}^4$
 

Rivet capacity in shear (single shear)
$R_s = 2(A_s \, \tau) = 2 \, [ \, \frac{1}{4}\pi (19^2)(100) \, ]$

$R_s = 18\,050\pi \, \text{ N} = 56.705 \, \text{ kN}$
 

Rivet capacity in bearing (use σ_b = 220 MPa)
$R_b = 2(A_b \, \sigma_b) = 2 \, [ \, 19(13.2)(220) \, ]$

$R_b = 110\,352 \, \text{ N} = 110.352 \, \text{ kN}$
 

Use R = 56.705 kN for safe value of R
 

From strength of rivets
$R = \dfrac{VQ_{NA}}{I}s$

$56.705 = \dfrac{V \, [ \, 7570(19.7) \, ]}{13\,555\,682.6}(200)$

$V = 25.77 \, \text{ kN}$           answer