Solution to Problem 594 | Spacing of Rivets or Bolts in Built-Up Beams

Problem 594
A distributed load of w_o lb/ft is applied over a middle 6 ft of a simply supported span 12 ft long. The beam section is that in Prob. 593, but used here so that the 8-in dimension is vertical. Determine the maximum value of w_o if f_b ≤ 1200 psi, f_v ≤ 120 psi, and the screws have a shear strength of 200 lb and a pitch of 2 in.
 

Solution 594
$M_{max} = 3(3w_o) + \frac{1}{2}(3)(3w_o)$

$M_{max} = 13.5w_o \, \text{ lb}\cdot\text{ft}$
 

 

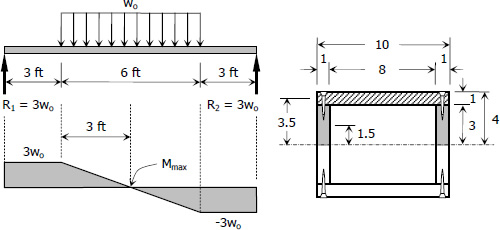
$I = \dfrac{10(8^3)}{12} - \dfrac{8(6^3)}{12}$

$I = 848/3 \, \text{ in}^3$
 

Based on allowable flexure stress:
$f_b = \dfrac{Mc}{I}$

$1200 = \dfrac{13.5w_o(12)(4)}{848 / 3}$

$w_o = 523.46 \, \text{ lb/ft}$
 

Based on shear stress of wood:
$f_v = \dfrac{VQ_{NA}}{Ib}$

$120 = \dfrac{3w_o \, [ \, 10(1)(3.5) + 3(1)(1.5)(2) \, ]}{(848 / 3)(2)}$

$w_o = 513.94 \, \text{ lb/ft}$
 

Based on shear strength of screws:
$s = \dfrac{RI}{VQ}$

$2 = \dfrac{(200 \times 2)(848 /3)}{3w_o \, [ \, 10(1)(3.5) \, ]}$

$w_o = 538.41 \, \text{ lb/ft}$
 

For safe value of w_o, use w_o = 513.94 lb/ft.           answer