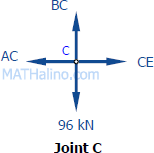
At Joint
C:
$\Sigma F_V = 0$
$BC = 96 \, \text{kN}$ (Tension)
Consider the section through member BD, BE, and CE:
$\Sigma M_A = 0$
$8(\frac{3}{5}BE) = 4(96)$
$BE = 80 \, \text{kN}$ (Compression)
For Member BC:
Based on shearing of rivets:
$BC = \tau A$ Where A = area of 1 rivet × number of rivets, n
$96\,000 = 70 [ \, \frac{1}{4} \pi (19^2) n \, ]$
$n = 4.8$ say 5 rivets
Based on bearing of member:
$BC = \sigma_b \, A_b$ Where Ab = rivet diameter × thickness of BC × n rivets
$96\,000 = 140 [ \, 19(6)n \, ]$
$n = 6.02$ say 7 rivets
Use 7 rivets for member BC. answer
For member BE:
Based on shearing of rivets:
$BE = \tau \, A$ Where A = area of 1 rivet × number of rivets, n
$80\,000 = 70 [ \, \frac{1}{4} \pi (19^2)n \, ]$
$n = 4.03$ say 5 rivets
Based on bearing of member:
$BE = \sigma_b \, A_b$ Where Ab = rivet diameter × thickness of BE × n rivets
$80\,000 = 140 [ \, 19(13)n \, ]$
$n = 2.3$ say 3 rivets
Use 5 rivets for member BE. answer
Relevant data from the table (Appendix B of textbook): Properties of Equal Angle Sections: SI Units
| Designation |
Area |
| L75 × 75 × 6 |
864 mm2 |
| L75 × 75 × 13 |
1780 mm2 |
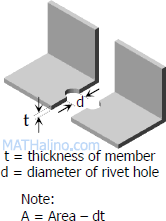Tensile stress of member BC (L75 × 75 × 6):
$\sigma = \dfrac{P}{A} = \dfrac{96(1000)}{864 - 19(6)}$
$\sigma = 128 \, \text{Mpa}$ answer
Compressive stress of member BE (L75 × 75 × 13):
$\sigma = \dfrac{P}{A} = \dfrac{80(1000)}{1780}$
$\sigma = 44.94 \, \text{Mpa}$ answer
Good day. I would like to ask
Good day. I would like to ask a clarification max tensile/compressive stress on the members.
Why did we use A=Area-dt for member BC, but for member BE, we just used the given area of 1780?
Maraming salamat po.
The member BE is in
In reply to Good day. I would like to ask by Mang Johnny (not verified)
The member BE is in compression, thus the whole cross-section is effective. The load transfers through the main area + bearing area, as the fastener is pressed against the hole area. Imagine as if the fastener was "clenched" between two semicircles representing a hole halves. The compression load transfers through the fastener further.
The member BC is in tension. In static analysis this check is commonly referred as "Net Area Tension stress" and accounts for the holes area (and usually stress concentration, but it's omitted here), that needs to be excluded from a gross (total) area. In this scenario, the fastener is pressed against either side, but the opposite hole side extends away from it and deforms in oval shape (it is in tension, remember?). Thus this hole area doesn't contribute into the total strength (imagine if there were no fasteners at all, but only holes), so we exclude it. It acts as a perforated toilet paper :D