Unanswered Forum Posts

[(1-xy)^-2]dx + [y^2-x^2(1-xy)^-2]dy=0 ;when x=1, y=1

I've been trying to solve the following question for 2 days now and i can't seem to be able to. can someone help me please ?

For the beam shown in Figure 3, the support at A is fully fixed. The beam is tapered however you may consider it to be a beam of 3 varying sections.

Take:
Beam A to B as having 3 times the I value of beam D to end, Beam B to D as having 1.5 times the I value of beam D to end and Beam D to end is 310 UB 46.2 with I = 100 x 106 mm4. Tip: this may be easier to solve using superposition.

1. y(x^2+xy-2y^2)dx+x(3y^2-xy-x^2)dy=0
2. (x+ysin y/x)dx-xsin y/x dy=0

Show that if f and f' are continuous on a ≤ x ≤ b and f(x) is not zero for all x on a ≤ x ≤ b,
then f and xf are linearly independent on a ≤ x ≤ b.

A spherical container of negligible thickness holding a hot fluid at 1400
and having
an outer diameter of 0.4 m is insulated with three layers of each 50 mm thick
insulation of k1 = 0.02: k2 = 0.06 and k3 = 0.16 W/mK. (Starting from inside). The
outside surface temperature is 300C. Determine (i) the heat loss, and (ii) Interface
temperatures of insulating layers.

need explaination plss..

Help please.
(1+e^(x) y+x e^(x) y) dx + (x e^(x) + 2) dy=0

The problem2x5y'=y(3x to the 4+y squred =0

please help me with this!!!
Im really having hard time getting this.
Region 1 is bounded by the x axis, the line x=1 and the curve y=x^2. Region 2 is bounded by the two curves y=x^2 and x=y^2. Region 3 is bounded by the y axis, the line y=1 and the curve x=y^2. Find the volume and centroid of the solid generated when the indicated region is revolved about the given line:
A. Region 1 is revolved about y axis
Region 1 is revolved about x axis
B. Region 2 is revolved about y axis
Region 2 is revolved about x axis

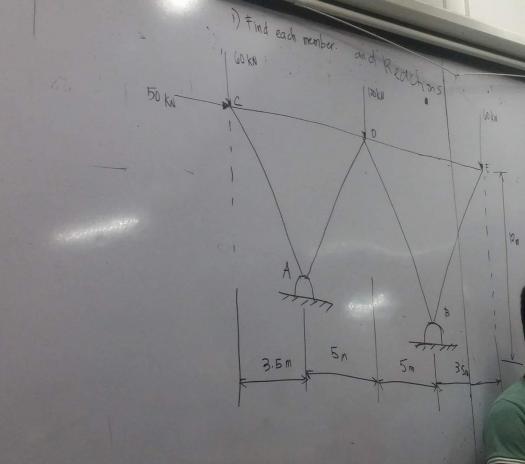
Find each member and reactions. (by joint method)