Active forum topics
- The Chain Rule Explained: Don't Just Memorize, Visualize It
- The Intuition Behind Integration by Parts (Proof & Example)
- Statics
- Calculus
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Application of Differential Equation: Newton's Law of Cooling
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
New forum topics
- The Chain Rule Explained: Don't Just Memorize, Visualize It
- The Intuition Behind Integration by Parts (Proof & Example)
- Statics
- Calculus
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
- Integration of 4x^2/csc^3x√sinxcosx dx
Recent comments
- Bakit po nagmultiply ng 3/4…1 month 2 weeks ago
- Determine the least depth…11 months 2 weeks ago
- Solve mo ang h manually…1 month 2 weeks ago
- Paano kinuha yung height na…11 months 4 weeks ago
- It's the unit conversion…1 year ago
- Refer to the figure below…1 year ago
- where do you get the sqrt411 month 2 weeks ago
- Thank you so much1 month 2 weeks ago
- How did you get the 2.8 mins…1 month 2 weeks ago
- How did you get the distance…1 month 2 weeks ago


I don't really know how to
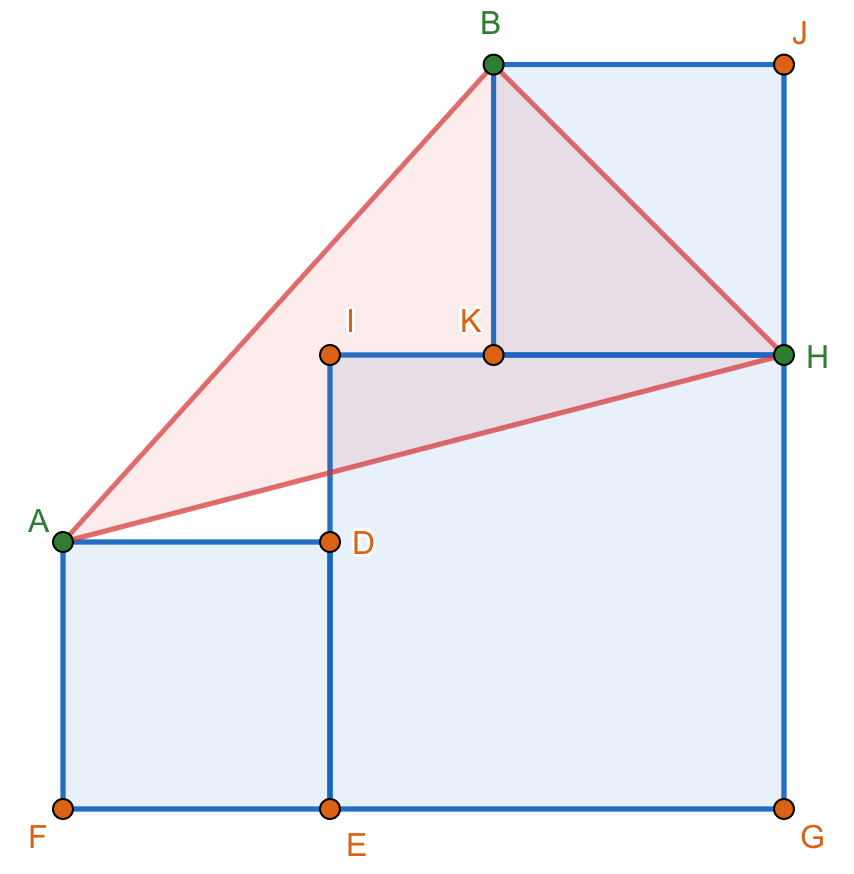
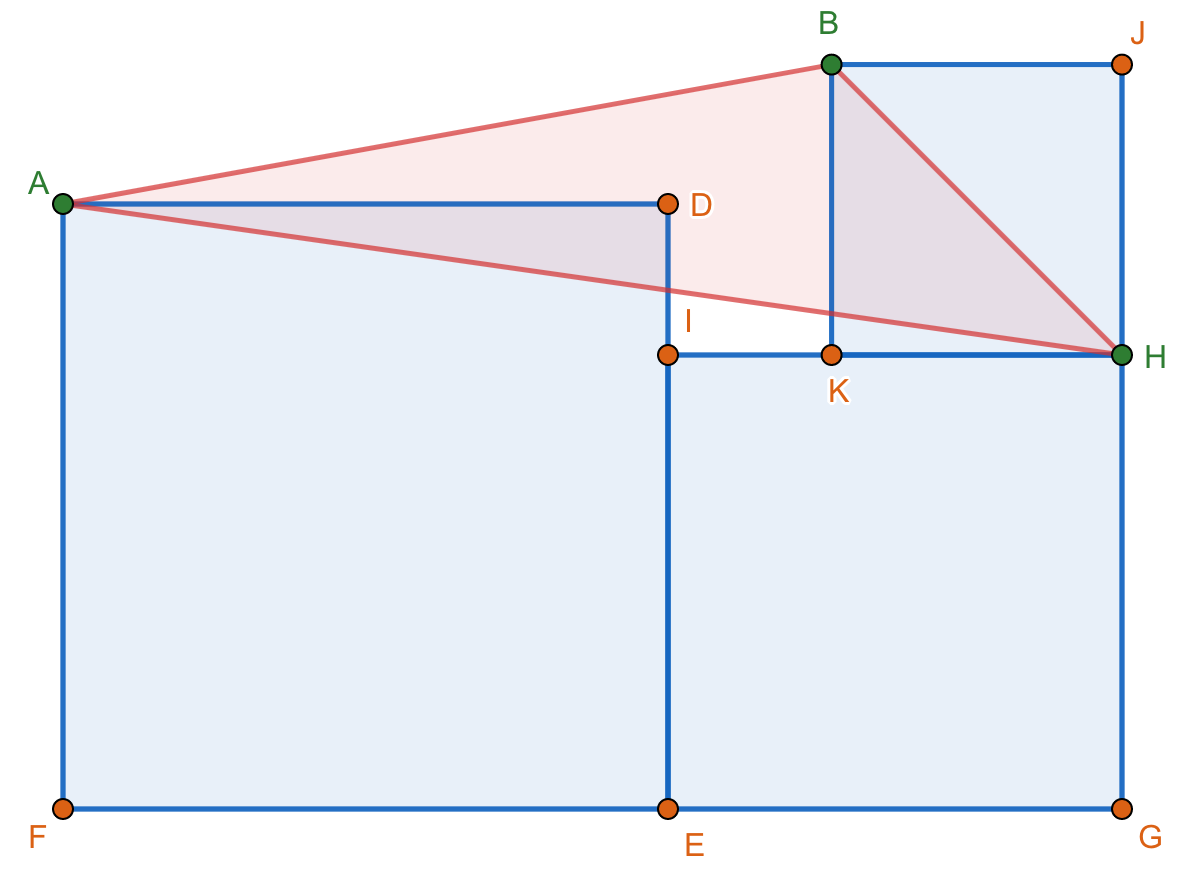
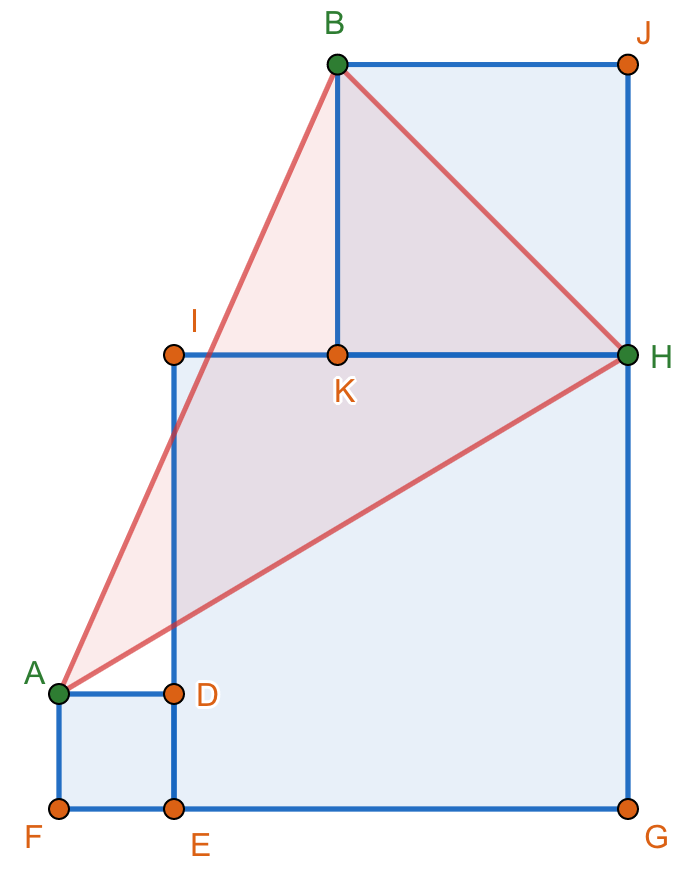
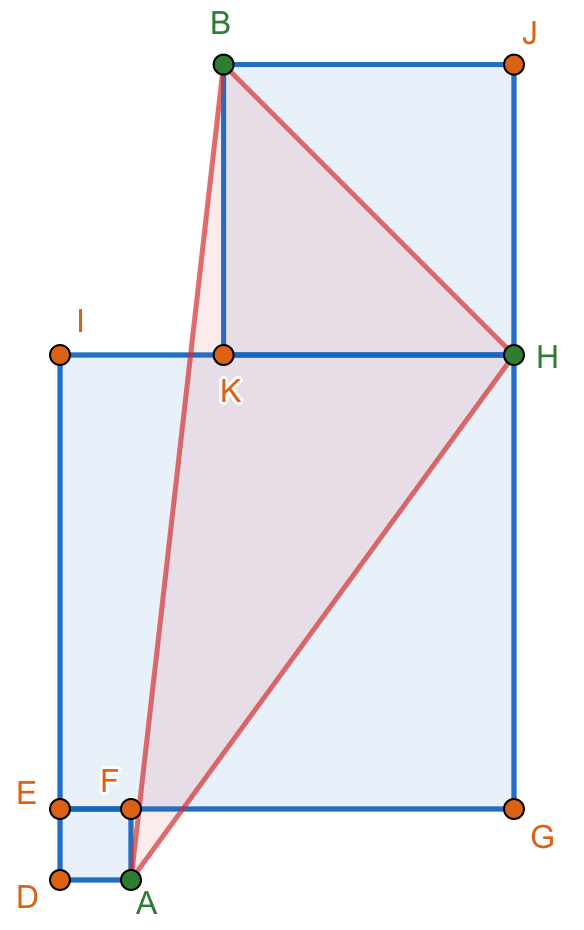
I don't really know how to prove this one sir. I just noticed when i substituted values, by taking line BH as the base, we will be having the same height in all triangles which we all know that if two triangles have the same base and height, their areas will be the same if i will not be mistaken.
Yes you are right. What you
In reply to I don't really know how to by MONGOL○482
Yes you are right. What you have in mind is the correct proof. All you need to do is to express it, the best is if you can articulate it through words and equations.
1. If we draw a line that
In reply to Yes you are right. What you by Jhun Vert
1. The diagonals of a square are perpendicular to each other.
2. If we draw a line extending diagonal AE of square AFED, we can see that vertex A is still going to land on this line no matter what the size of square AFED.
3. We can also see that diagonal AE is perpendicular to diagonal BH since their bases are parallel on the horizon lets say x.
Having these in mind and setting BH as the base of the triangle, and since vertex A can also land on vertex E, we can say that Area ABH=1/2 (BH)(EG2+GH2)1/2