Solution to Problem 630 | Moment Diagrams by Parts
Problem 630
For the beam loaded as shown in Fig. P-630, compute the value of (AreaAB)barred(X)A . From the result determine whether the tangent drawn to the elastic curve at B slopes up or down to the right. (Hint: Refer to the deviation equations and rules of sign.)
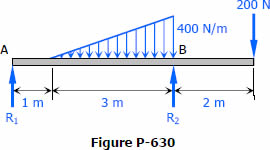
- Read more about Solution to Problem 630 | Moment Diagrams by Parts
- Log in or register to post comments




Recent comments