Spiral Curve

Spirals are used to overcome the abrupt change in curvature and superelevation that occurs between tangent and circular curve. The spiral curve is used to gradually change the curvature and superelevation of the road, thus called transition curve.
 

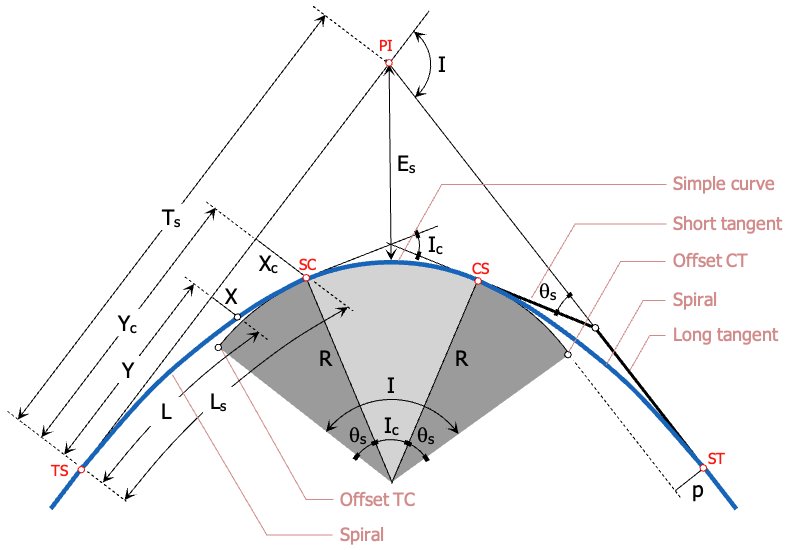
Elements of Spiral Curve

• TS = Tangent to spiral
• SC = Spiral to curve
• CS = Curve to spiral
• ST = Spiral to tangent
• LT = Long tangent
• ST = Short tangent
• R = Radius of simple curve
• T_s = Spiral tangent distance
• T_c = Circular curve tangent
• L = Length of spiral from TS to any point along the spiral
• L_s = Length of spiral
• PI = Point of intersection
• I = Angle of intersection
• I_c = Angle of intersection of the simple curve
• p = Length of throw or the distance from tangent that the circular curve has been offset
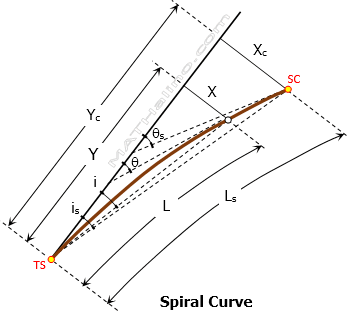
• X = Offset distance (right angle distance) from tangent to any point on the spiral
• X_c = Offset distance (right angle distance) from tangent to SC
• Y = Distance along tangent to any point on the spiral
• Y_c = Distance along tangent from TS to point at right angle to SC
• E_s = External distance of the simple curve
• θ = Spiral angle from tangent to any point on the spiral
• θ_s = Spiral angle from tangent to SC
• i = Deflection angle from TS to any point on the spiral, it is proportional to the square of its distance
• i_s = Deflection angle from TS to SC
• D = Degree of spiral curve at any point
• D_c = Degree of simple curve

Formulas for Spiral Curves

Distance along tangent to any point on the spiral:
$Y = L - \dfrac{L^5}{40R^2{L_s}^2}$
 

At L = L_s, Y = Y_c, thus,
$Y_c = L_s - \dfrac{{L_s}^3}{40R^2}$
 

Offset distance from tangent to any point on the spiral:
$X = \dfrac{L^3}{6RL_s}$
 

At L = L_s, X = X_c, thus,
$X_c = \dfrac{{L_s}^2}{6R}$
 

Length of throw:
$p = \frac{1}{4}X_c = \dfrac{{L_s}^2}{24R}$
 

Spiral angle from tangent to any point on the spiral (in radian):
$\theta = \dfrac{L^2}{2RL_s}$
 

At L = L_s, θ = θ_s, thus,
$\theta_s = \dfrac{L_s}{2R}$
 

Deflection angle from TS to any point on the spiral:
$i = \frac{1}{3}\theta = \dfrac{L^2}{6RL_s}$
 

At L = L_s, i = i_s, thus,
$i = \frac{1}{3}\theta_s = \dfrac{L_s}{6R}$
 

This angle is proportional to the square of its distance
$\dfrac{i}{i_s} = \dfrac{L^2}{{L_s}^2}$
 

Tangent distance:
$T_s = \dfrac{L_s}{2} + (R + P)\tan \dfrac{I}{2}$
 

Angle of intersection of simple curve:
$I_c = I - 2\theta_s$
 

External distance:
$E_s = \dfrac{R + P}{\cos \dfrac{I}{2}} - R$
 

Degree of spiral curve:
$\dfrac{D}{D_C} = \dfrac{L}{L_s}$