Beams with Different Materials
From assumption no. (3) in the previous page: The strains of any two adjacent materials at their junction point are equal.
$\epsilon_s = \epsilon_w$
$\dfrac{f_{bs}}{E_s} = \dfrac{f_{bw}}{E_w}$
$\dfrac{f_{bs}}{f_{bw}} = \dfrac{E_s}{E_w}$
We let the moduli ratio be equal to n
$n = \dfrac{E_s}{E_w}$
It will follow also that the equivalent wood stress of the transformed steel is
$f_{b-\text{wood equivalent}} = \dfrac{f_{bs}}{n}$
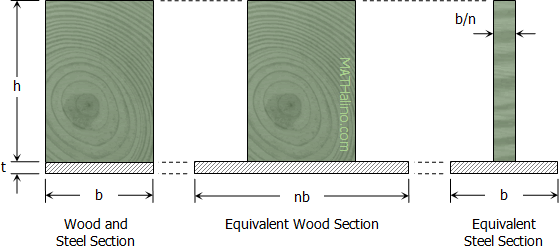
From assumption no. (4): The loads carried by equivalent fibers are equal.
$P_w = P_s$
$f_{bw} \, A_w = f_{bs} \, A_s$
$A_w = \dfrac{f_{bs}}{f_{bw}} \cdot A_s$
$A_w = \dfrac{E_s}{E_w} \cdot A_s$
The equivalent area of steel in wood is
$A_w = n \, A_s$
Tags