composite beam

Problem
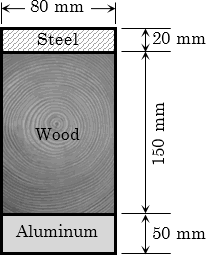
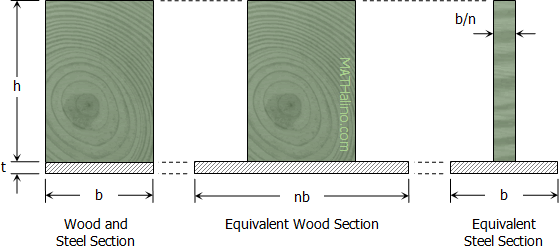
Steel and aluminum plates are used to reinforced an 80 mm by 150 mm timber beam. The three materials are fastened firmly as shown so that there will be no relative movement between them.
 

Given the following material properties:

Find the safe resisting moment of the beam in kN·m.
 

Problem 1003
A simply supported beam 4 m long has the cross section shown in Fig. P-1002. It carries a uniformly distributed load of 20 kN/m over the middle half of the span. If n = 15, compute the maximum stresses in the wood and the steel.
 

Problem 1004
Repeat Problem 1002 assuming that the reinforcement consists of aluminum plates for which the allowable stress is 80 MPa. Use n = 5.
 

Problem 1002
A timber beam is reinforced with steel plates rigidly attached at the top and bottom as shown in Fig. P-1002. By what amount is moment increased by the reinforcement if n = 15 and the allowable stresses in the wood and steel are 8 MPa and 120 MPa, respectively?
 

From assumption no. (3) in the previous page: The strains of any two adjacent materials at their junction point are equal.
$\epsilon_s = \epsilon_w$

$\dfrac{f_{bs}}{E_s} = \dfrac{f_{bw}}{E_w}$

$\dfrac{f_{bs}}{f_{bw}} = \dfrac{E_s}{E_w}$
 

Flexure formula do not apply directly to composite beams because it was based on the assumption that the beam was homogeneous. It is therefore necessary to transform the composite material into equivalent homogeneous section. To do this, consider a steel and wood section to be firmly bolted together so that they can act as one unit. Shown below are the composite wood and steel section and the corresponding equivalent in wood and steel sections.
 

The quantity n is usually taken as the ratio of the moduli of elasticity of stronger material to the weaker material. In the above case, n = E_s / E_w.