Discharge or Flow Rate

Discharge (also called flow rate)
The amount of fluid passing a section of a stream in unit time is called the discharge. If v is the mean velocity and A is the cross sectional area, the discharge Q is defined by Q = Av which is known as volume flow rate. Discharge is also expressed as mass flow rate and weight flow rate.

Where:
Q = discharge in m³/sec or ft³/sec
A = cross-sectional area of flow in m² or ft²
v = mean velocity of flow in m/sec or ft/sec
ρ = mass density of fluid in kg/m³ or slugs/ft³
γ = unit weight of fluid in N/m³ or lb/ft³
 

Laminar Flow
Flow is said to be laminar when the paths of the individual particles do not cross or intersect. By many careful experiments to commercial pipes of circular cross section, the flow is laminar when the Reynolds’ number Re is less than 2100.
 

Turbulent Flow
The flow is said to be turbulent when its path lines are irregular curves and continuously cross each other. The paths of particles of a stream flowing with turbulent motion are neither parallel nor fixed but it aggregates to forward motion of the entire stream. Reynolds’ number greater than 2100 normally defines turbulent flow but in highly controlled environment such as laboratories, laminar flow can be maintained up to values of Re as high as 50,000. However, it is very unlikely that such condition can occur in the practice.
 

Steady Flow
Steady flow occurs if the discharge Q passing a given cross section of a stream is constant with time, otherwise the flow is unsteady.
 

Uniform Flow
The flow is said to be uniform if, with steady flow for a given length, or reach, of a stream, the average velocity at every cross-section is the same. Uniform flow usually occurs to incompressible fluids flowing in a stream of constant cross section. In streams where velocity and cross section changes, the flow is said to be non-uniform.
 

Continuous Flow
By the principle of conservation of mass, continuous flow occurs when at any time, the discharge Q at every section of the stream is the same.
 

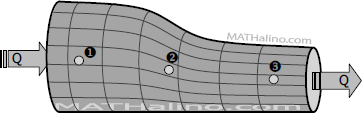
Continuity Equations
For incompressible fluids:

For compressible fluids: