Please help me solve this problem: Moment capacity of a rectangular timber beam

Submitted by candybutcher on

A timber was planned to be use as a floor beam to support the loads shown. The section was initially designed to have the dimensions shown. For timber its flexural stress is limited to 27.6 mPa. Is the initial design enough to support the load? If not what should be its depth “d”, if the architect wished to maintain the breadth “b” of 100mm?

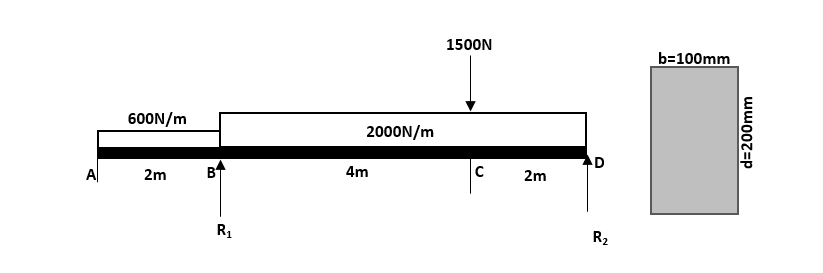
asdasdasd.png

Questions:

1) Detailed and correct solution/computations of reactions
2) Detailed and correct solution/computations of Shear Values
3) Detailed and correct solution/computations of Moment Values
4) Detailed and correct Shear and Moment diagrams
5) Test for flexural capacity of the beam
6) Re-designing as to required depth “d” if failed

Tags
Shear Values
Moment Values
Shear and Moment diagrams

Jhun Vert Sat, 01/02/2021 - 11:05

How is your solution to this problem? Which part do you have difficulty in solving? Here is what you are going to do:

  • For number (1), use $\Sigma M_D = 0$ to solve for $R_1$ and $\Sigma M_B$ for $R_2$
  • Items (2), (3) and (4) can be done with just (4). By showing the shear and moment diagram, you already get the (2) and (3) answered.
  • For number (5), I think the instruction is not worded precisely because the flexural capacity is already given which is 27.6 MPa. I think the question is about the maximum moment capacity, it is practical to interpret it this way. With this, just use the flexure formula for rectangular section which is $f_b = \dfrac{6M}{bd^2}$, and solve for M while holding fb at 27.6 MPa. The value of M will be the maximum moment capacity of the beam.
  • Compare the maximum moment you get from from (5) to the maximum moment you get in you shear and moment diagram which are the actual moments. Of course if the largest actual moment is larger than that in number (5) then your section is inadequate and you need a deeper beam, re-design your beam with adequate $d$ per instruction. However if the largest moment in your diagram is less than or equal to the moment in (5) then no need to redesign because the section is already good to go in terms of moment capacity