solid mensuration

#1

To find the volume, lateral and total surface area of the square pyramid shown below:

Let's get the volume of the pyramid first.

The volume of the right pyramid is:

$$V = \frac{1}{3}Bh$$

where $V$ is the volume of the pyramid, $B$ is the area of the base and $h$ is the height of the right pyramid.

With that in mind, the volume would be:

$$V = \frac{1}{3}Bh$$ $$V = \frac{1}{3}(5 \space units \times 5 \space units)(18 \space units)$$ $$V = 150 \space cubic \space units$$

The volume of the square pyramid above is $\color{red}{150 \space cubic \space units}$.

Let's get the lateral surface area of the pyramid above.

The lateral surface area of the right pyramid is:

$$LSA = \frac{1}{2}(Perimeter \space of \space base)(Slant \space height)$$

With that in mind, the lateral surface area of the pyramid is:

Notice that we don't have the slant height, so we need to get the slant height. Now getting the slant height:

$$(slant \space height)^2 = 18^2 + 2.5^2$$ $$slant \space height = 18.2 \space units$$

Now getting the lateral surface area:

$$LSA = \frac{1}{2}(Perimeter \space of \space base)(Slant \space height)$$ $$LSA = \frac{1}{2}(5 \space units + 5 \space units +5 \space units + 5 \space units)(18.2 \space units)$$ $$LSA = 182 \space square \space units$$

Therefore, the lateral surface area of the square pyramid above is $\color{blue}{182 \space square \space units}$.

Let's get the total surface area of the square pyramid above.

The total surface area of the square pyramid is the lateral surface area of the pyramid plus the area of the base.

Now getting the total surface area:

$$TSA = LSA + B$$

We got the lateral surface area ($182 \space square \space units$). We don't have the area of the base. The area of the base is $5 \space units \times 5 \space units$ or $25 \space square \space units$.

The total surface area (TSA) of the square pyramid above is:
$$TSA = LSA + B$$ $$TSA = 182 \space square \space units+25 \space square \space units$$ $$\color{green}{TSA = 207 \space square \space units}$$

#2

To find the volume, lateral and total surface area of the rectangular pyramid shown below:

Let's get the volume of the pyramid first.

The volume of the right pyramid is:

$$V = \frac{1}{3}Bh$$

where $V$ is the volume of the pyramid, $B$ is the area of the base and $h$ is the height of the right pyramid.

Notice that we don't have the height of the pyramid, so we need to get it. Now getting the height of rectangular pyramid:

$$30^2 = h^2 + \frac{7.2}{2}^2$$ $$h = 29.8 \space units$$

The volume would be:

$$V = \frac{1}{3}Bh$$ $$V = \frac{1}{3}(6 \space units \times 4 \space units)(29.8 \space units)$$ $$V = 238.4 \space cubic \space units$$

The volume of the rectangular pyramid above is $\color{red}{238.4 \space cubic \space units}$

Let's get the lateral surface area of the rectangular pyramid above.

The lateral surface area of the right pyramid is:

$$LSA = \frac{1}{2}(Perimeter \space of \space base)(Slant \space height)$$

This time though, we can't straighforwardly get the lateral surface area of the rectangular pyramid using the formula above. Instead, the lateral surface area of the rectangular pyramid is total area of the lateral sides of the rectangular pyramid.

Now getting the area of one side of the rectangular pyramid:

$$(Slant \space height)^2 + 3^2 = 30^2$$ $$Slant \space height = 29.8 \space units$$

The area of this triangle will be:

$$Area = \frac{1}{2}bh$$ $$Area = \frac{1}{2}(3 \space units)(29.8 \space units)h$$ $$Area = 44.7 \space units^2$$

The area of the whole side of this rectangular pyramid is:

$$2 \times Area = Area_1 = 89.4 \space units^2$$

Now getting the area of another side of the rectangular pyramid:

$$(Slant \space height)^2 + 2^2 = 30^2$$ $$Slant \space height = 29.9 \space units$$

The area of this triangle will be:

$$Area = \frac{1}{2}bh$$ $$Area = \frac{1}{2}(2 \space units)(29.9 \space units)$$ $$Area = 29.9 \space units^2$$

The area of the whole side of this rectangular pyramid is:

$$2 \times Area = Area_2 = 59.8 \space units^2$$

We can now get the lateral surface area of the pyramid. The lateral surface area would be:

$$LSA = 2\times Area_1 + 2\times Area_2$$ $$LSA = 2(89.4 \space units^2) + 2(59.8 \space units^2)$$ $$LSA = 298.4 \space units^2$$

Therefore, the lateral surface area of the rectangular pyramid is $\color{blue}{298.4 \space units^2}$.

Let's get the total surface area of the rectangular pyramid above.

The total surface area of the rectangular pyramid is the lateral surface area of the pyramid plus the area of the base.

Now getting the total surface area:

$$TSA = LSA + B$$

We got the lateral surface area ($316.4 \space square \space units$). We don't have the area of the base. The area of the base is $6 \space units \times 4 \space units$
or $24 \space square \space units$.

The total surface area (TSA) of the rectangular pyramid above is:
$$TSA = LSA + B$$ $$TSA = 316.4 \space square \space units+24 \space square \space units$$ $$\color{green}{TSA = 340.4 \space square \space units}$$

#3

To find the volume, lateral and total surface area of the equilateral pyramid shown below:

Let's get the volume of the pyramid first.

The volume of the right pyramid is:

$$V = \frac{1}{3}Bh$$

where $V$ is the volume of the pyramid, $B$ is the area of the base and $h$ is the height of the right pyramid.

Notice that we don't have the height of the pyramid, so we need to get it. Now getting the height of equilateral pyramid:

Looking at the base of the pyramid:

$$\frac{y}{10} = \tan 30^o$$ $$y = 5.8 \space cm$$

Now looking at the side of the pyramid containing the line $y$:

$$40^2 = h^2 + y^2$$ $$40^2 = h^2 + (5.8)^2$$ $$h = 39.6 \space cm$$

Now getting the area of the base of equilateral pyramid:

$$Area = \frac{\sqrt{3}}{4}a^2$$

Then...

$$Area = \frac{\sqrt{3}}{4}(20 \space cm)^2$$ $$Area = 173.2 \space cm^2$$

The volume would be:

$$V = \frac{1}{3}Bh$$ $$V = \frac{1}{3}(173.2 \space cm^2)(39.6 \space cm)$$ $$V = 2286.2\space cubic \space cm$$

The volume of the equilateral pyramid above is $\color{red}{2286.2 \space cubic \space cm}$

Let's get the lateral surface area of the equilateral pyramid above.

The lateral surface area of the right pyramid is:

$$LSA = \frac{1}{2}(Perimeter \space of \space base)(Slant \space height)$$
This time though, we can't straighforwardly get the lateral surface area of the equilateral pyramid using the formula above. Instead, the lateral surface area of the equilateral pyramid is total area of the lateral sides of the equilateral pyramid.

Now getting the area of one side of the equilateral pyramid:

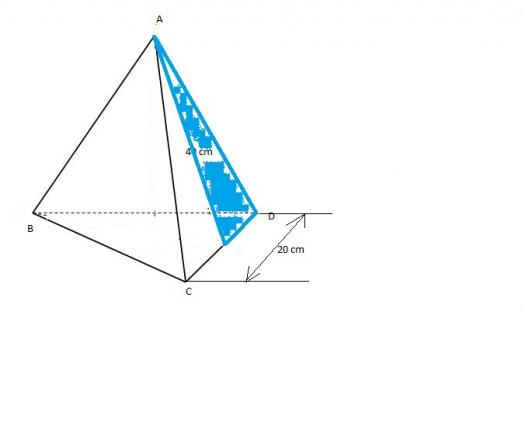
$$(Slant \space height)^2 + 10^2 = 40^2$$ $$Slant \space height = 38.7 \space cm$$

The area of this triangle will be:

$$Area = \frac{1}{2}(base)(slant \space height)$$ $$Area = \frac{1}{2}(10 \space cm)(38.7 \space cm)$$ $$Area = 193.5 \space cm^2$$

The area of the whole side of this equilateral pyramid is:

$$2 \times Area = Area_1 = 387 \space cm^2$$

Now getting the lateral surface area of equilateral pyramid:

$$3 \times Area_1 = 1161 cm^2$$

Therefore, the lateral surface area of the equilateral pyramid is $\color{blue}{1161 \space cm^2}$.

Let's get the total surface area of the equilateral pyramid above.

The total surface area of the rectangular pyramid is the lateral surface area of the pyramid plus the area of the base.

Now getting the total surface area:

$$TSA = LSA + B$$

We got the lateral surface area ($1161 \space square \space cm$). We also got the area of the base ($173.2 cm^2$)

The total surface area (TSA) of the equilateral pyramid above is:
$$TSA = LSA + B$$ $$TSA = 1161 \space square \space cm^2 + 173.2 \space square \space cm$$ $$\color{green}{TSA = 1334.2 \space square \space cm}$$

Alternate solutions are encouraged.....

Grabeh haba nun. Tatlong oras tinayp yun ah....

Malabo po yung picture. Baka mali sagot ko....hehehe