Mechanics
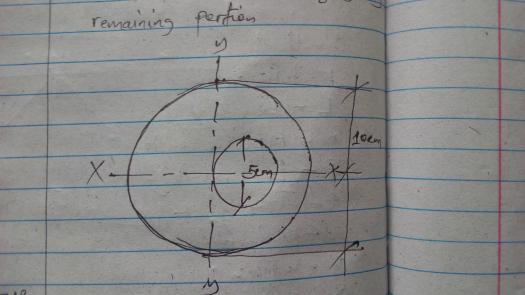
From the circular disk of diameter 100mm is cut out a circle whose diameter is the radius of the disk. F ind the center of gravity of remaining portion.
- Log in to post comments
 MATHalinoEngineering Math Review
MATHalinoEngineering Math ReviewFrom the circular disk of diameter 100mm is cut out a circle whose diameter is the radius of the disk. F ind the center of gravity of remaining portion.

 Forum posts (unless otherwise specified) licensed under a Creative Commons Licence.
Forum posts (unless otherwise specified) licensed under a Creative Commons Licence.
Ah! You mean this?
Ah! You mean this?
To get the coordinates of centroid of the figure above, we need to use the formula
$$A \bar x = A_1x_1 + A_2x_2 + A_3x_3 +A_4x_4 +....A_n x_n$$ $$A \bar y = A_1y_1 + A_2y_2 + A_3y_3 +A_4y_4 +....A_n y_n$$
where:
$A = $ area of the whole figure
$x = $ distance of the centroid from the $x$-axis
$A_1 = $ area of one part of the figure
$x_1 = $ distance of its particular centroid from the $x$-axis
.
.
.
.
.
.
$y = $ distance of the centroid from the $y$-axis
$A_1 = $ area of one part of the figure
$y_1 = $ distance of its particular centroid from the $y$-axis
The formula that is applicable to the figure above would be:
$$A \bar x = A_1x_1 + A_2x_2 + A_3x_3 +A_4x_4 $$ $$A \bar y = A_1y_1 + A_2y_2 + A_3y_3 +A_4y_4 $$
Redrawing the figure to make things clearer:
Now getting the A, A$_1$, A$_2$, A$_3$, A$_4$:
For A:
$$A = \pi R^2 - \pi r^2$$ $$A = \pi (5 \space cm)^2 - \pi (2.5 \space cm)^2$$ $$A = 25\pi \space cm^2 - 6.25\pi \space cm^2$$ $$A = 18.75\pi \space cm^2$$
For A$_1$:
$$A_1 = \frac{25}{4}\pi \space cm^2 - \frac{6.25}{2}\pi\space cm^2$$ $$A_1 = 3.125\pi \space cm^2$$
For A$_4$:
$$A_4 = \frac{25}{4}\pi \space cm^2 - \frac{6.25}{2}\pi\space cm^2$$ $$A_4 = 3.125\pi \space cm^2$$
For A$_2$:
$$A_2 = \frac{25}{4}\pi \space cm^2$$
For A$_3$:
$$A_3 = \frac{25}{4}\pi \space cm^2$$
Now getting the x, x$_1$, x$_2$, x$_3$, x$_4$:
For x:
We can get it after I got x$_1$, x$_2$, x$_3$, x$_4$
For x$_1$:
Then the centroidal coordinates of A$_1$ is:
$$ x_1 = 0.3488 r$$ $$ x_1 = (0.3488) (5 \space cm)$$ $$ x_1 = 1.744 \space cm$$
The real value of $\bar x$ is:
$$\bar x_1 = 5 + 1.744 \space cm = 6.744 \space cm$$
For x$_2$
The centroidal coordinates of a quarter circle is:
$$\bar x = \frac{4}{3\pi} r$$ $$\bar y = \frac{4}{3\pi} r$$
Then the centroidal coordinates of A$_2$
$$ x_2 = \frac{4}{3\pi} r$$ $$ x_2 = \frac{4}{3\pi} (5 \space cm)$$ $$ x_2 = 2.1 \space cm$$
The real value of $x_2$ is:
$$x_3 = 5-2.1 \space cm = 2.9 \space cm$$
For x$_3$:
The centroidal coordinates of a quarter circle is:
$$ x = \frac{4}{3\pi} r$$ $$ y = \frac{4}{3\pi} r$$
Then the centroidal coordinates of A$_3$
$$ x_3 = \frac{4}{3\pi} r$$ $$ x_3 = \frac{4}{3\pi} (5 \space cm)$$ $$ x_3 = 2.1 \space cm$$
The real value of $x_3$ is:
$$x_3 = 5-2.1 \space cm = 2.9 \space cm$$
For x$_4$:
Then the centroidal coordinates of A$_4$ is:
$$ x_4 = 0.3488 r$$ $$ x_4 = (0.3488) (5 \space cm)$$ $$ x_4 = 1.744 \space cm$$
The real value of $ x_4$ is:
$$ x_4 = 5 + 1.744 \space cm = 6.74 \space cm $$
We can now get the $\bar x$:
$$A \bar x = A_1x_1 + A_2x_2 + A_3x_3 +A_4x_4 $$ $$(18.75\pi \space cm^2) \bar x = (3.125\pi \space cm^2)(6.744 \space cm) + (\frac{25}{4}\pi \space cm^2)(2.9 \space cm) + (\frac{25}{4}\pi \space cm^2)(2.9 \space cm) + (3.125\pi \space cm^2)(6.744 \space cm) $$ $$\bar x = 4.18 \space cm$$
To get the $\bar y$, notice that the figure is symmetrical, so the $\bar y$ centroidal coordinate would be $0$
Therefore, the centroid $C(\bar x, \bar y)$ of the figure above would be $C(\bar x, \bar y) = C(4.18, 0)$
Alternate solutions are encouraged:-)