shear and moment diagram
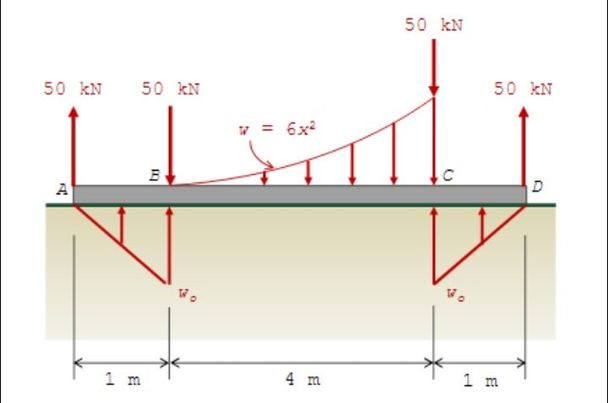
A. determine Wo
B. Draw the shear and moment diagrams and specify the numerical values at all change of loading positions & at all points of zero shear.
C. determine the maximum shear and maximum moment.
- Log in to post comments


First, it looks like this