How old is Ann?

Submitted by Angkol-Awin on

The combined ages of Mary and Ann are 44 years.
Mary is twice as old as Ann was when Mary was half
as old as Ann will be when Ann is three times as old as Mary
was when Mary was three times as old as Ann.
How old is Ann?

Tags
Age Problem

Engr Jaydee Wed, 06/16/2021 - 16:37
solution_1.png solution_2.png Answer: 66/7 years old. The answer does not make sense to me, though. When I also checked it, the value of z is negative, which is weird. Please reply if you have corrections to my solution. Thanks! :)

Angkol-Awin Tue, 07/20/2021 - 07:40
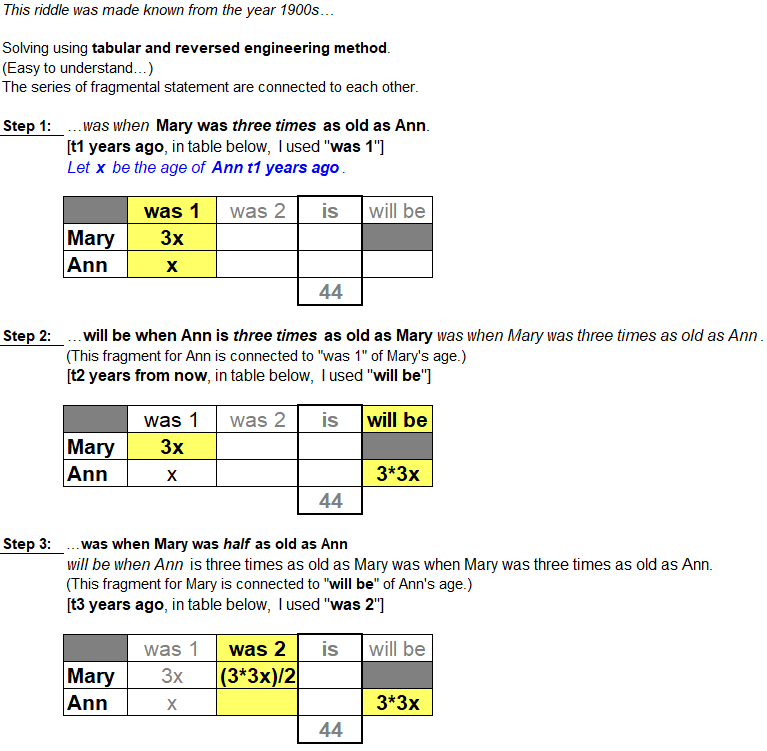
Hi Sir, For the first highlighted phrase, "...was when Mary was three times as old as Ann is now." There is no "is now" from the problem. Hint 1: This problem / riddle was made popular from around the year 1900. Hint 2: Mary is 27 years and 6 months (1/2 year). Hint 3: I solved this using tabular method.

smaricic Mon, 09/06/2021 - 03:27
Well, they say great minds think alike. And we all agree that our minds are great, right? Years ago, I stumbled on the "How old is Ann?" puzzle while thumbing through an old copy of Bartlett's Familiar Quotations. During the current pandemic, with some time on my hands, I decided to make a somewhat humorous YouTube based on that puzzle. It took me a lot longer than I thought it would, but I finally posted it. When I searched for it last week, I was pleasantly surprised to learn that folks at Mathalino had worked on it, too -- although yours is somewhat different from my 1903 version. You might get a kick out of my video: https://www.youtube.com/watch?v=KzyZz5UqCXs Best wishes, Steve Maricic