Active forum topics
- The Chain Rule Explained: Don't Just Memorize, Visualize It
- The Intuition Behind Integration by Parts (Proof & Example)
- Statics
- Calculus
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Application of Differential Equation: Newton's Law of Cooling
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
New forum topics
- The Chain Rule Explained: Don't Just Memorize, Visualize It
- The Intuition Behind Integration by Parts (Proof & Example)
- Statics
- Calculus
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
- Integration of 4x^2/csc^3x√sinxcosx dx
Recent comments
- Bakit po nagmultiply ng 3/4…1 month 2 weeks ago
- Determine the least depth…11 months 2 weeks ago
- Solve mo ang h manually…1 month 2 weeks ago
- Paano kinuha yung height na…11 months 3 weeks ago
- It's the unit conversion…1 year ago
- Refer to the figure below…1 year ago
- where do you get the sqrt411 month 2 weeks ago
- Thank you so much1 month 2 weeks ago
- How did you get the 2.8 mins…1 month 2 weeks ago
- How did you get the distance…1 month 2 weeks ago

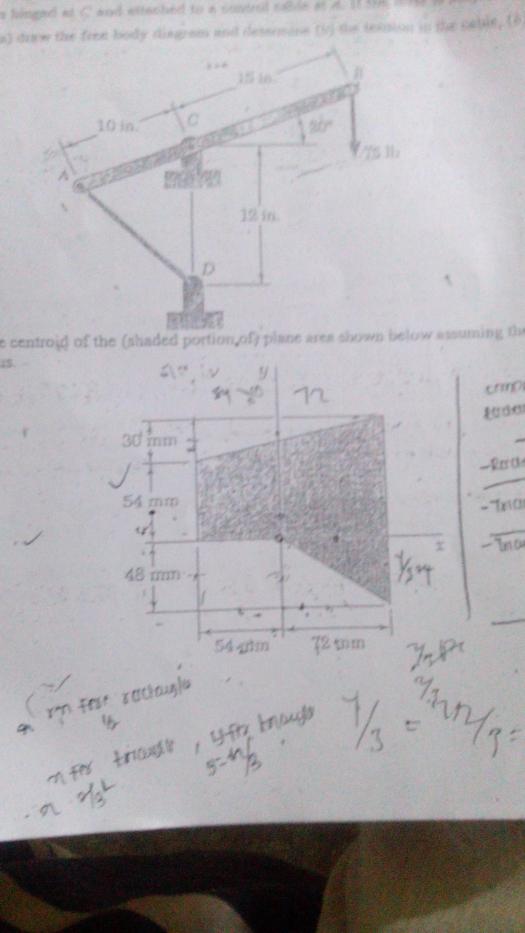 please
please
$A_1 = 126(54) = 6,804 ~
$A_1 = 126(54) = 6,804 ~ \text{mm}^2$
$x_1 = \frac{1}{2}(126) - 54 = 9 ~ \text{mm}$
$y_1 = \frac{1}{2}(54) = 27 ~ \text{mm}$
$A_2 = \frac{1}{2}(126)(30) = 1,890 ~ \text{mm}^2$
$x_2 = \frac{2}{3}(126) - 54 = 30 ~ \text{mm}$
$y_2 = 54 + \frac{1}{3}(30) = 64 ~ \text{mm}$
$A_3 = \frac{1}{2}(72)(48) = 1,728~ \text{mm}^2$
$x_3 = \frac{2}{3}(72) = 48 ~ \text{mm}$
$y_3 = -\frac{1}{3}(48) = -16 ~ \text{mm}$
$A = \Sigma A_n = 6,804 + 1,890 + 1,728$
$A = 10,422 ~ \text{mm}^2$
$\bar{x} = \dfrac{\Sigma A_n x_n}{A} = \dfrac{6804(9) + 1890(30) + 1728(48)}{10\,422}$
$\bar{y} = \dfrac{\Sigma A_n y_n}{A} = \dfrac{6804(27) + 1890(64) - 1728(16)}{10\,422}$