Circle
Good day po sir! Is the angle of intersection between two chords of a circle equal to one of the vertical angles of the cyclic quadrilateral that is formed by this chords? Im so confused. Please help. Below is the problem followed with my progression. Thanks a ton!


- Log in to post comments


Good day po sir! Is the angle
If you mean diagonals for chords, the answer is no. Imagine a rectangle inscribed in a circle, the angle at the vertex of the rectangle is 90° but the angle between diagonals is not 90°.
No sir. I mean if for e.g.
In reply to Good day po sir! Is the angle by Jhun Vert
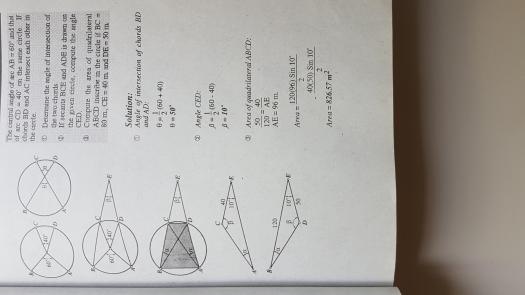
No sir. I mean if for e.g. angle theta is the angle of intersection of two intersecting chords in a circle, AC & BD, will this angle change if i drew a secant line BCE & ADE? I seem to have a problem getting the area of the quadrilateral if i resolve it into triangles. Im so confused right now. Please help sir. Thank you so much
If you extend your chords so
In reply to Good day po sir! Is the angle by Jhun Vert
If you extend your chords so that it will become intersecting secants, the intersection angle of diagonals won't change, it will remain the same. Intersection angle will only change if you relocate at least one of the vertices of your cyclic quadrilateral, changing the central angle of the arcs of circle. If the arc angles are constant, like 60 degrees and 40 degrees in the problem you uploaded, the intersection angle won't change. I can't give you a mathematical proof for now but I will upload a screenshot I made in Geogebra.
The areas you presented supposed to equate to each other. I can't see the details of your work, the picture you posted I think is too large and the system resize its width. Try to upload your solution in separate pictures in a portrait (or standing) orientation.
In reply to Good day po sir! Is the angle by Jhun Vert
Figure 1
Figure 2
Figure 3
Good am sir! Please let me
In reply to by Jhun Vert
Good am sir! Please let me know when you see the images.
Yes it is all clear now. Here
In reply to by Jhun Vert
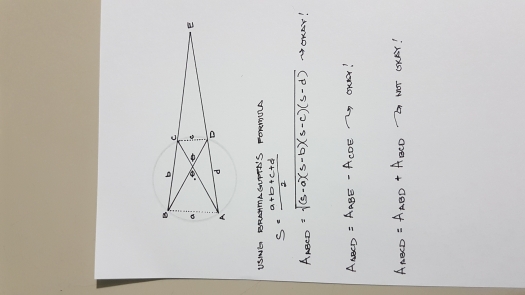
Yes it is all clear now. Here is my solution, I did the area of cyclic quadrilateral though, not two adjacent triangles.
Yes sir, but if i try to
In reply to Yes it is all clear now. Here by Jhun Vert
Yes sir, but if i try to solve for Angle CAE by getting diagonal AC and using cosine law or sine law, im getting the value 6.995 degrees instead of 20 degrees. Please help me sir find my mistake.
You need the fundamental
In reply to Yes it is all clear now. Here by Jhun Vert
You need the fundamental principle of the relationship between central angle and included angle. The angle you are trying to find needs no calculation. I recommend you read this page. https://www.mathalino.com/reviewer/plane-geometry/relationship-between-…
Thank you sir. I checked on
In reply to You need the fundamental by Jhun Vert
Thank you sir. I checked on it.
I also tried solving for the area of the cyclic quadrilateral by adding the area of the triangles ABD & BCD but it leads me to an incorrect answer. Is this method against the rules sir? I dont know what im missing.
No it is not against the rule
In reply to You need the fundamental by Jhun Vert
No it is not against the rule. In fact, that is the very method I used to solve non-cyclic quadrilaterals. Instead of using a long formula, two triangles are more convenient.
Thank you for the
In reply to No it is not against the rule by Jhun Vert
Thank you for the confirmation sir. I'll be checking on it. GBU always!