March 2017
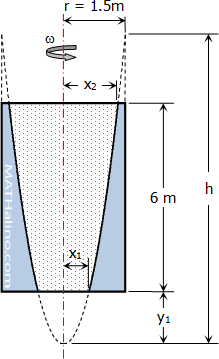
Rotation - Rotating Vessel
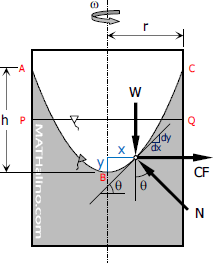
When at rest, the surface of mass of liquid is horizontal at PQ as shown in the figure. When this mass of liquid is rotated about a vertical axis at constant angular velocity ω radian per second, it will assume the surface ABC which is parabolic. Every particle is subjected to centripetal force or centrifugal force CF = mω2x which produces centripetal acceleration towards the center of rotation. Other forces that acts are gravity force W = mg and normal force N.
- Read more about Rotation - Rotating Vessel
- Log in to post comments
Relative Equilibrium of Liquids
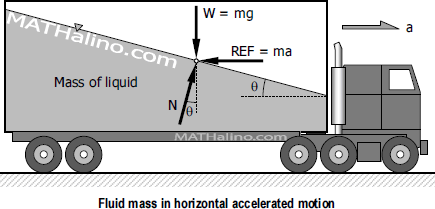
Relative equilibrium of liquid is a condition where the whole mass of liquid including the vessel in which the liquid is contained, is moving at uniform accelerated motion with respect to the earth, but every particle of liquid have no relative motion between each other. There are two cases of relative equilibrium that will be discussed in this section: linear translation and rotation. Note that if a mass of liquid is moving with constant speed, the conditions are the same as static liquid in the previous sections.
- Read more about Relative Equilibrium of Liquids
- Log in to post comments
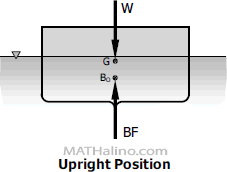
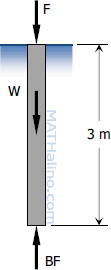
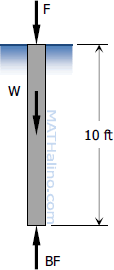
Stability of Floating Bodies
Any floating body is subjected by two opposing vertical forces. One is the body's weight W which is downward, and the other is the buoyant force BF which is upward. The weight is acting at the center of gravity G and the buoyant force is acting at the center of buoyancy BO. W and BF are always equal and if these forces are collinear, the body will be in upright position as shown below.
- Read more about Stability of Floating Bodies
- Log in to post comments
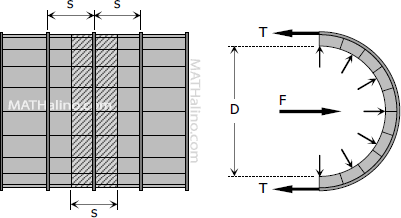
Stresses on Thin-walled Pressure Tanks
The circumferential stress, also known as tangential stress, in a tank or pipe can be determined by applying the concept of fluid pressure against curved surfaces. The wall of a tank or pipe carrying fluid under pressure is subjected to tensile forces across its longitudinal and transverse sections.
- Read more about Stresses on Thin-walled Pressure Tanks
- Log in to post comments
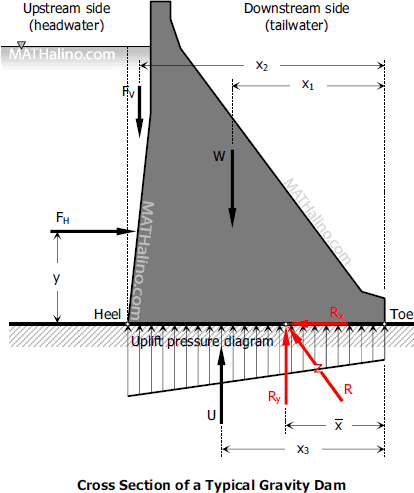
Analysis of Gravity Dam
Dams are structures whose purpose is to raise the water level on the upstream side of river, stream, or other waterway. The rising water will cause hydrostatic force which will tend the dam to slide horizontally and overturn about its downstream edge or toe. The raised water level on the upstream edge or heel will also cause the water to seep under the dam. The pressure due to this seepage is commonly called hydrostatic uplift and will reduce the stability of the dam against sliding and against overturning.
- Read more about Analysis of Gravity Dam
- Log in to post comments
Problem 01 - Buoyancy
- Read more about Problem 01 - Buoyancy
- Log in to post comments
Buoyancy
- Read more about Buoyancy
- Log in to post comments
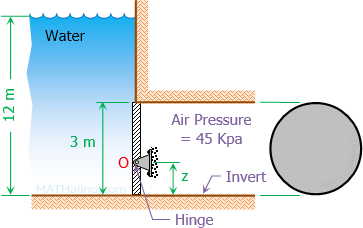
Circular Gate with Water on One Side and Air on the Other Side
Situation
The figure below shows a vertical circular gate in a 3-m diameter tunnel with water on one side and air on the other side.
- Find the horizontal reaction at the hinge.
A. 412 kN
B. 408 kN
C. 410 kN
D. 414 kN - How far from the invert of the tunnel is the hydrostatic force acting on the gate?
A. 1.45 m
B. 1.43 m
C. 1.47 m
D. 1.41 m - Where will the hinge support be located (measured from the invert) to hold the gate in position?
A. 1.42 m
B. 1.46 m
C. 1.44 m
D. 1.40 m