Rotation - Rotating Vessel

When at rest, the surface of mass of liquid is horizontal at PQ as shown in the figure. When this mass of liquid is rotated about a vertical axis at constant angular velocity ω radian per second, it will assume the surface ABC which is parabolic. Every particle is subjected to centripetal force or centrifugal force CF = mω2x which produces centripetal acceleration towards the center of rotation. Other forces that acts are gravity force W = mg and normal force N.
 

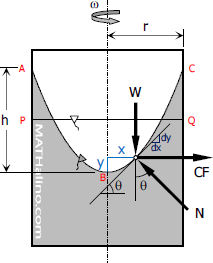
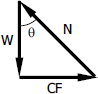
008-rotating-vessel.gif                     008-force-polygon.gif

 

$\tan \theta = \dfrac{CF}{W}$

$\tan \theta = \dfrac{m\omega^2x}{mg}$
 

$\tan \theta = \dfrac{\omega^2x}{g}$

Where tan θ is the slope at the surface of paraboloid at any distance x from the axis of rotation.
 

From Calculus, y’ = slope, thus
$\dfrac{dy}{dx} = \tan \theta$

$\dfrac{dy}{dx} = \dfrac{\omega^2x}{g}$

$dy = \dfrac{\omega^2}{g}x ~ dx$

$\displaystyle \int dy = \dfrac{\omega^2}{g} \int x ~ dx$

$y = \dfrac{\omega^2x^2}{2g}$

 

For cylindrical vessel of radius r revolved about its vertical axis, the height h of paraboloid is

$h = \dfrac{\omega^2r^2}{2g}$

 

Other Formulas
By squared-property of parabola, the relationship of y, x, h and r is defined by

$\dfrac{r^2}{h} = \dfrac{x^2}{y}$

 

Volume of paraboloid of revolution

$V = \frac{1}{2}\pi r^2h$

 

Important conversion factor

$1 \, \text{ rpm} = \frac{1}{30}\pi \, \text{ rad/sec}$

 

Tags
centrifugal force
angular velocity
paraboloid
squared property of parabola
Centripetal Acceleration
slope of paraboloid
Volume of Paraboloid