Rectilinear Translation - Moving Vessel

Horizontal Motion
If a mass of fluid moves horizontally along a straight line at constant acceleration a, the liquid surface assume an angle θ with the horizontal, see figure below.
 

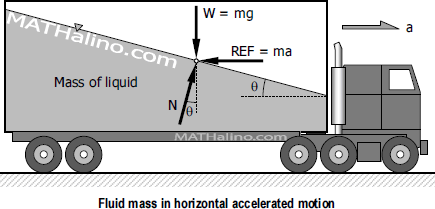
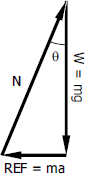For any value of a, the angle θ can be found by considering a fluid particle of mass m on the surface. The forces acting on the particle are the weight W = mg, inertia force or reverse effective force REF = ma, and the normal force N which is the perpendicular reaction at the surface. These three forces are in equilibrium with their force polygon shown to the right.
 

From the force triangle
$\tan \theta = \dfrac{REF}{W}$

$\tan \theta = \dfrac{ma}{mg}$

Inclined Motion
Consider a mass of fluid being accelerated up an incline α from horizontal. The horizontal and vertical components of inertia force REF would be respectively, x = ma_h and y = ma_v.
 

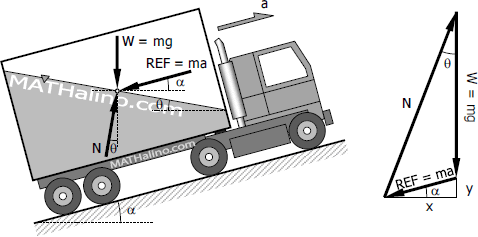
From the force triangle above
$\tan \theta = \dfrac{x}{W + y}$

$\tan \theta = \dfrac{ma \cos \alpha}{mg + ma \sin \alpha}$

$\tan \theta = \dfrac{a \cos \alpha}{g + a \sin \alpha}$
 

but a cos α = a_h and a sin α = a_v, hence
$\tan \theta = \dfrac{a_h}{g + a_v}$

Use (+) sign for upward motion and (-) sign for downward motion.
 

Vertical Motion
The figure shown to the right is a mass of liquid moving vertically upward with a constant acceleration a. The forces acting to a liquid column of depth h from the surface are weight of the liquid W = γV, the inertia force REF = ma, and the pressure F = pA at the bottom of the column.
 

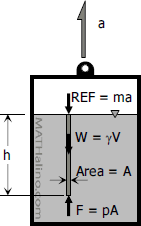$\Sigma F_V = 0$

$F = W + REF$

$pA = \gamma V + ma$

$pA = \gamma V + \rho Va$

$pA = \gamma V + \dfrac{\gamma}{g} Va$

$pA = \gamma (Ah) + \dfrac{\gamma}{g} (Ah)a$

$p = \gamma h + \dfrac{\gamma}{g} ha$

$p = \gamma h \left(1 + \dfrac{a}{g}\right)$

Use (+) sign for upward motion and (-) sign for downward motion. Also note that a is positive for acceleration and negative for deceleration.