March 2017
Problem 03 - Bernoulli's Energy Theorem
Problem 3
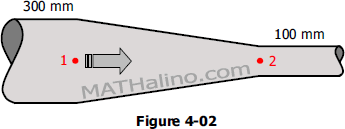
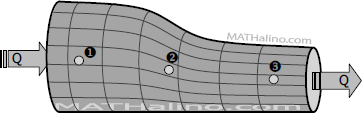
A 300-mm pipe is connected by a reducer to a 100-mm pipe. See Figure 4-02. Points 1 and 2 are at the same elevation, the pressure at 1 is 200 kPa. The discharge Q is 30 liters per second flowing from 1 to 2 and the energy lost from 1 to 2 is equivalent to 20 kPa.
- Compute the pressure at 2 if the liquid is water.
- Compute the pressure at 2 if the liquid is oil (sp gr = 0.80).
- Compute the pressure at 2 if the liquid is molasses (sp gr = 1.5).
- Read more about Problem 03 - Bernoulli's Energy Theorem
- Log in to post comments
Problem 02 - Bernoulli's Energy Theorem
Problem 2
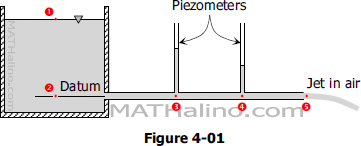
From Figure 4-01, the following head losses are known: From (1) to (2), 0 m; from (2) to (3), 0.60 m; from (3) to (4), 2.1 m; from (4) to (5), 0.3 m. Make a table showing elevation head, velocity head, pressure head, and total head at each of the five points. How high above the center of the pipe will water stands in the piezometer tubes (3) and (4)?
- Read more about Problem 02 - Bernoulli's Energy Theorem
- Log in to post comments
Energy and Head of Flow
Energy is defined as ability to do work. Both energy and work are measured in Newton-meter (or pounds-foot in English). Kinetic energy and potential energy are the two commonly recognized forms of energy. In a flowing fluid, potential energy may in turn be subdivided into energy due to position or elevation above a given datum, and energy due to pressure in the fluid. Head is the amount of energy per Newton (or per pound) of fluid.
Kinetic Energy and Velocity Head
Kinetic energy is the ability of a mass to do work by virtue of its velocity. The kinetic energy of a mass M having a velocity v is ½Mv2. Since M = W/g,
$\text{Velocity head} = \dfrac{K.E.}{W} = \dfrac{v^2}{2g}$
Elevation Energy and Elevation Head
In connection to the action of gravity, elevation energy is manifested in a fluid by virtue of its position or elevation with respect to a horizontal datum plane.
$\text{Elevation head} = \dfrac{\text{Elevation energy}}{W} = z$
Pressure Energy and Pressure Head
A mass of fluid acquires pressure energy when it is in contact with other masses having some form of energy. Pressure energy therefore is an energy transmitted to the fluid by another mass that possesses some energy.
$\text{Pressure head} = \dfrac{\text{Pressure energy}}{W} = \dfrac{p}{W}$
- Read more about Energy and Head of Flow
- Log in to post comments
02 Graph of flow velocity in tapering pipe
Problem
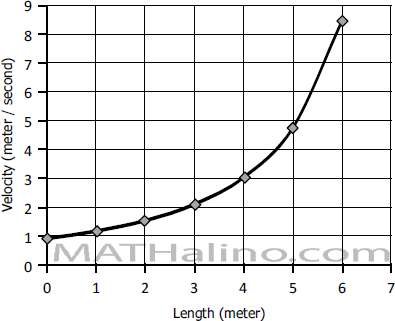
The diameter of a 6-m length pipe decreases uniformly from 450 mm to 150 mm. With a flow of 0.15 m3/sec of oil, compute the mean velocity at cross section 1 m apart. Plot the velocity as ordinate against length as abscissa.
Graph of velocity of flow versus length of pipe (plotted in MS Excel)
- Read more about 02 Graph of flow velocity in tapering pipe
- Log in to post comments
01 How to calculate the discharge and the velocity of flow
Problem 1
Compute the discharge of water through 75 mm pipe if the mean velocity is 2.5 m/sec.
Problem 2
The discharge of air through a 600-mm pipe is 4 m3/sec. Compute the mean velocity in m/sec.
Problem 3
A pipe line consists of successive lengths of 380-mm, 300-mm, and 250-mm pipe. With a continuous flow through the line of 250 Lit/sec of water, compute the mean velocity in each size of pipe.
Discharge or Flow Rate
Discharge (also called flow rate)
The amount of fluid passing a section of a stream in unit time is called the discharge. If v is the mean velocity and A is the cross sectional area, the discharge Q is defined by Q = Av which is known as volume flow rate. Discharge is also expressed as mass flow rate and weight flow rate.
Mass flow rate, $M = \rho Q$
Weight flow rate, $W = \gamma Q$
- Read more about Discharge or Flow Rate
- Log in to post comments
Fundamentals of Fluid Flow
Principles relating to fluids at rest can be obtained with no ambiguity by purely rational methods. Some natural principles which are universally true are the basis of calculations. In flowing fluid, however, the laws that govern the motion are complex and most of the time defies mathematical expressions. Thanks to experimental data combined with mathematical theories which solved countless engineering problems in the past.
- Read more about Fundamentals of Fluid Flow
- Log in to post comments