Spherical Wedge and Spherical Lune
A spherical wedge is a solid formed by revolving a semi-circle about its diameter by less than 360°. Spherical Lune is the curve surface of the wedge, it is a surface formed by revolving a semi-circular arc about its diameter by less than 360°.
- Read more about Spherical Wedge and Spherical Lune
- Log in to post comments
Spherical Sector
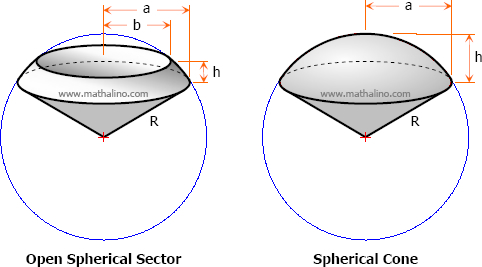
A spherical sector is a solid generated by revolving a sector of a circle about an axis which passes through the center of the circle but which contains no point inside the sector. If the axis of revolution is one of the radial sides, the sector thus formed is spherical cone; otherwise, it is open spherical sector.
- Read more about Spherical Sector
- Log in to post comments
Spherical Segment
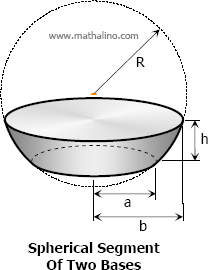
Spherical segment is a solid bounded by two parallel planes through a sphere. In terms of spherical zone, spherical segment is a solid bounded by a zone and the planes of a zone's bases.
- Read more about Spherical Segment
- Log in to post comments
Spherical Zone
Zone
A zone is that portion of the surface of the sphere included between two parallel planes.
- Read more about Spherical Zone
- Log in to post comments
The Sphere
Sphere is a solid bounded by closed surface every point of which is equidistant from a fixed point called the center.
- Read more about The Sphere
- Log in to post comments
The Right Circular Cone
Any cone with circular right section is a circular cone. Right circular cone is a circular cone whose axis is perpendicular to its base.
- Read more about The Right Circular Cone
- Log in to post comments
Frustum of a Right Circular Cone
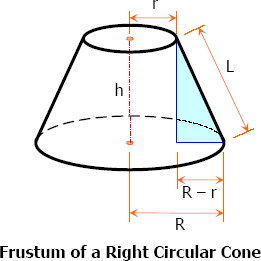
Frustum of a right circular cone is that portion of right circular cone included between the base and a section parallel to the base not passing through the vertex.
- Read more about Frustum of a Right Circular Cone
- Log in to post comments
Frustum of a Regular Pyramid
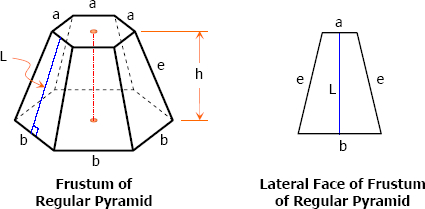
Frustum of a regular pyramid is a portion of right regular pyramid included between the base and a section parallel to the base.
- Read more about Frustum of a Regular Pyramid
- Log in to post comments
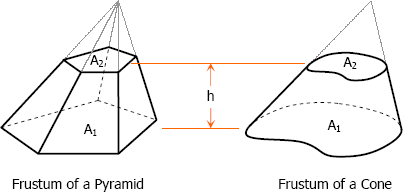
Frustums
Frustum of a pyramid (or cone) is a portion of pyramid (or cone) included between the base and the section parallel to the base not passing through the vertex.
- Read more about Frustums
- Log in to post comments
The Cone
Cone
The surface generated by a moving straight line (generator) which always passes through a fixed point (vertex) and always intersects a fixed plane curve (directrix) is called conical surface. Cone is a solid bounded by a conical surface whose directrix is a closed curve, and a plane which cuts all the elements. The conical surface is the lateral area of the cone and the plane which cuts all the elements is the base of the cone.
- Read more about The Cone
- Log in to post comments