Centers of a Triangle
This page will define the following: incenter, circumcenter, orthocenter, centroid, and Euler line.
Incenter
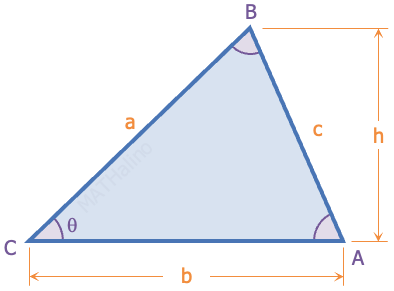
Incenter is the center of the inscribed circle (incircle) of the triangle, it is the point of intersection of the angle bisectors of the triangle.

The radius of incircle is given by the formula
where At = area of the triangle and s = ½ (a + b + c). See the derivation of formula for radius of incircle.
- Read more about Centers of a Triangle
- Log in to post comments

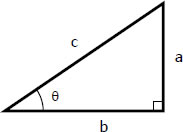 a/c = sin θ
a/c = sin θ