For Beams (B - 3) | Solution to Problem 542
For Beams (B - 3)
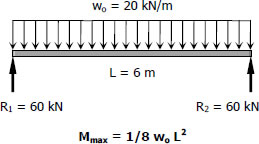$M_{max} = \frac{1}{8}(20)(62)$
$M_{max} = 90 \, \text{kN}\cdot\text{m}$
$S_{required} = \dfrac{M_{max}}{f_b} = \dfrac{90(1000^2)}{120}$
$S_{required} = 750 \times 10^3 \, \text{mm}^3$
- Read more about For Beams (B - 3) | Solution to Problem 542
- Log in or register to post comments
For Beams (B - 2) | Solution to Problem 542
For Beams (B - 2)
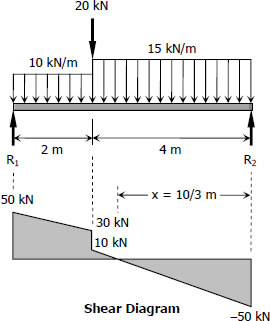$\Sigma M_{R2} = 0$
$6R_1 = 20(4) + 10(2)(5) + 15(4)(2)$
$R_1 = 50 \, \text{kN}$
$\Sigma M_{R1} = 0$
$6R_2 = 20(2) + 10(2)(1) + 15(4)(4)$
$R_2 = 50 \, \text{kN}$
- Read more about For Beams (B - 2) | Solution to Problem 542
- 1 comment
- Log in or register to post comments
For Girder (G - 1) | Solution to Problem 542
For Girder (G - 1)
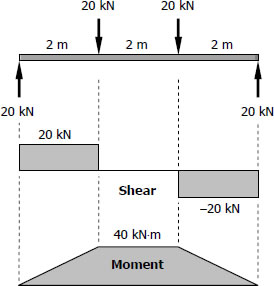$S_{live-load} = \dfrac{M}{f_b} = \dfrac{40(1000^2)}{120}$
$S_{live-load} = 333.33 \times 10^3 \, \text{mm}^3$
- Read more about For Girder (G - 1) | Solution to Problem 542
- Log in or register to post comments
Solution to Problem 542 | Floor Framing
Problem 542
Select the lightest W shape sections that can be used for the beams and girders in Illustrative Problem 537 of text book if the allowable flexural stress is 120 MPa. Neglect the weights of the members.
- Read more about Solution to Problem 542 | Floor Framing
- Log in or register to post comments
Solution to Problem 541 | Floor Framing
Problem 541
The 18-ft long floor beams in a building are simply supported at their ends and carry a floor load of 0.6 lb/in2. If the beams have W10 × 30 sections, determine the center-line spacing using an allowable flexural stress of 18 ksi.
- Read more about Solution to Problem 541 | Floor Framing
- Log in or register to post comments
Solution to Problem 540 | Floor Framing
Problem 540
Timbers 8 inches wide by 12 inches deep and 15 feet long, supported at top and bottom, back up a dam restraining water 9 feet deep. Water weighs 62.5 lb/ft3. (a) Compute the center-line spacing of the timbers to cause fb = 1000 psi. (b) Will this spacing be safe if the maximum fb, (fb)max = 1600 psi, and the water reaches its maximum depth of 15 ft?
- Read more about Solution to Problem 540 | Floor Framing
- Log in or register to post comments
Solution to Problem 539 | Floor Framing
Problem 539
Timbers 12 inches by 12 inches, spaced 3 feet apart on centers, are driven into the ground and act as cantilever beams to back-up the sheet piling of a coffer dam. What is the maximum safe height of water behind the dam if water weighs = 62.5 lb/ft3 and ( fb )max = 1200 psi?
- Read more about Solution to Problem 539 | Floor Framing
- Log in or register to post comments
Solution to Problem 538 | Floor Framing
Problem 538
Floor joists 50 mm wide by 200 mm high, simply supported on a 4-m span, carry a floor loaded at 5 kN/m2. Compute the center-line spacing between joists to develop a bending stress of 8 MPa. What safe floor load could be carried on a center-line spacing of 0.40 m?
- Read more about Solution to Problem 538 | Floor Framing
- Log in or register to post comments
Solution to Problem 536 | Economic Sections
Problem 536
A simply supported beam 10 m long carries a uniformly distributed load of 20 kN/m over its entire length and a concentrated load of 40 kN at midspan. If the allowable stress is 120 MPa, determine the lightest W shape beam that can be used.
- Read more about Solution to Problem 536 | Economic Sections
- Log in or register to post comments
Solution to Problem 535 | Economic Sections
Problem 535
A simply supported beam 24 ft long carries a uniformly distributed load of 2000 lb/ft over its entire length and a concentrated load of 12 kips at 8 ft from left end. If the allowable stress is 18 ksi, select the lightest suitable W shape. What is the actual maximum stress in the selected beam?
- Read more about Solution to Problem 535 | Economic Sections
- Log in or register to post comments