steel
Solution to Problem 133 Pressure Vessel
Problem 133
A cylindrical steel pressure vessel 400 mm in diameter with a wall thickness of 20 mm, is subjected to an internal pressure of 4.5 MN/m2. (a) Calculate the tangential and longitudinal stresses in the steel. (b) To what value may the internal pressure be increased if the stress in the steel is limited to 120 MN/m2? (c) If the internal pressure were increased until the vessel burst, sketch the type of fracture that would occur.
- Read more about Solution to Problem 133 Pressure Vessel
- Log in to post comments
Solution to Problem 131 Bearing Stress
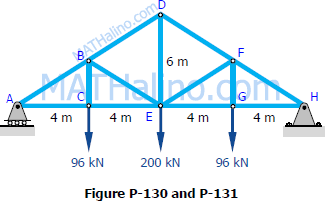
Problem 131
Repeat Problem 130 if the rivet diameter is 22 mm and all other data remain unchanged.
- Read more about Solution to Problem 131 Bearing Stress
- Log in to post comments
Solution to Problem 130 Bearing Stress
Problem 130
Figure P-130 shows a roof truss and the detail of the riveted connection at joint B. Using allowable stresses of τ = 70 MPa and σb= 140 MPa, how many 19-mm-diameter rivets are required to fasten member BC to the gusset plate? Member BE? What is the largest average tensile or compressive stress in BC and BE?
Solution to Problem 108 Normal Stress
Problem 108
An aluminum rod is rigidly attached between a steel rod and a bronze rod as shown in Fig. P-108. Axial loads are applied at the positions indicated. Find the maximum value of P that will not exceed a stress in steel of 140 MPa, in aluminum of 90 MPa, or in bronze of 100 MPa.
- Read more about Solution to Problem 108 Normal Stress
- Log in to post comments
Solution to Problem 107 Normal Stress
Problem 107
A rod is composed of an aluminum section rigidly attached between steel and bronze sections, as shown in Fig. P-107. Axial loads are applied at the positions indicated. If P = 3000 lb and the cross sectional area of the rod is 0.5 in2, determine the stress in each section.

- Read more about Solution to Problem 107 Normal Stress
- Log in to post comments
Solution to Problem 105 | Normal Stress
Problem 105
A homogeneous 800 kg bar AB is supported at either end by a cable as shown in Fig. P-105. Calculate the smallest area of each cable if the stress is not to exceed 90 MPa in bronze and 120 MPa in steel.
- Read more about Solution to Problem 105 | Normal Stress
- Log in to post comments