Solution to Problem 632 | Moment Diagrams by Parts
Problem 632
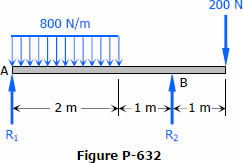
For the beam loaded as shown in Fig. P-632, compute the value of (AreaAB) barred(X)A. From this result, is the tangent drawn to the elastic curve at B directed up or down to the right? (Hint: Refer to the deviation equations and rules of sign.)