Limits

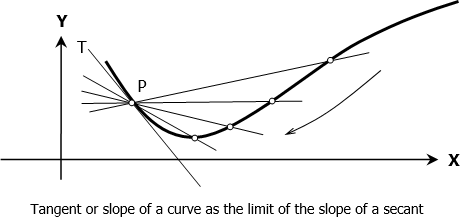
We can redefine Calculus as a branch of mathematics that enhances Algebra, Trigonometry, and Geometry through the limit process. Calculus simply will not exist without limits because every aspect of it is in the form of a limit in one sense or another. To illustrate this notion, consider a secant line whose slope is changing until it will become a tangent (or the slope of the curve) at point P (see figure below). Then we can say that the slope of the curve at any point P is the limit of the slope of the secant through P.
 

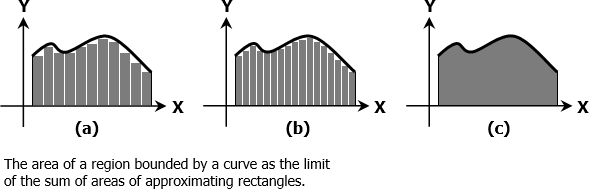
Another is by considering the area of a region bounded by curve shown in figures (a), (b), and (c) below. The area can be approximated by summing up the areas of series of rectangles. As the number of rectangles increases, the sum of their areas will be close enough to the area in (c). We can then say that the area of the region bounded by a curve is the limit of the sum of areas of approximating rectangles.
 

We can therefore define limit as a number such that the value of a given function remains arbitrarily close to this number when the independent variable is sufficiently close to a specified point.
 

Theorems on Limits

1. If $f(x) = c$, a constant, then $\displaystyle \lim_{x \to a} f(x) = c$.
    
2. $\displaystyle \lim_{x \to a} k \, f(x) = k \, \lim_{x \to a} f(x)$, k being constant.
    
3. $\displaystyle \lim_{x \to a} \left[ f(x) \pm g(x) \right] = \lim_{x \to a} f(x) \pm \lim_{x \to a} g(x)$
    
4. $\displaystyle \lim_{x \to a} \left[ f(x) \times g(x) \right] = \left[ \lim_{x \to a} f(x) \right] \times \left[ \lim_{x \to a} g(x) \right]$
    
5. $\displaystyle \lim_{x \to a} \left[ \dfrac{f(x)}{g(x)} \right] = \dfrac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}$, provided $\displaystyle \lim_{x \to a} g(x) \ne 0$
    
6. $\displaystyle \lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)}$, provided $\sqrt[n]{\lim_{x \to a} f(x)}$ is a real number.
    
7. $\displaystyle \lim_{x \to 0} \dfrac{\sin x}{x} = 1$, x is in radians.

L'Hospital’s Rule (Indeterminate type 0/0)
If $a$ is a number, if $f(x)$ and $g(x)$ are differentiable and $g(x) \ne 0$ for all $x$ on some interval $0 \lt \left| x - a \right| \lt \delta$, and if $\lim_{x \to a} f(x) = 0$ and $\lim_{x \to a} g(x) = 0$, then, when $\displaystyle \lim_{x \to a} \dfrac{f'(x)}{g'(x)}$ exists or is infinite,
 

where $f'(x)$ and $g'(x)$ are derivatives of $f(x)$ and $g(x)$, respectively.