Sets

Contents

  1. Elements of a Set
  2. Universal Set, U
  3. Null Set
  4. Subset
  5. Complement of a Set
  6. Disjoint Sets
  7. Union
  8. Intersection
  9. Difference
  10. Symmetric Difference

Definition
A set is a collection of explicitly-defined distinct elements.
 

Back to top

Elements of a Set

If 2, 4, 6, 8 are elements of A, we can then write

$A = \{0, ~ 2, ~ 4, ~ 6, ~ 8\}$

or it can be written using the set-builder notation

$A = \{x ~ : ~ x \text{ is an even digit} \}$

read as "A is the set of all x such that x is an even digit".
 

The phrase “2 is an element of A” is equivalent to the statement “2 belongs to A”. In symbol, we write

$2 \in A$

It follows that

$5 \notin A$

to indicate that “5 is not an element of A”.
 

Back to top

Universal Set, U

Universal set consists all elements under consideration.
 

a-universal-set.gif

 

Back to top

Null Set

An empty set, or a set with no element, is called a null set and is denoted by $\varnothing$.
 

$\varnothing = \{ ~ \}$

 

Back to top

Subset

If all elements of set A belongs to set B, then A is a subset of B. In symbol we write

$A \subseteq B$   or   $B \supseteq A$

to respectively indicate that "A is contained in B" or "B contains A".
 

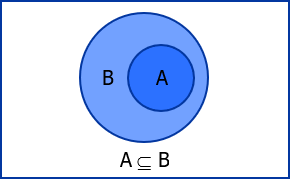
a-subset-b.gif

 

The negation of this is

$A \nsubseteq B$

 

Example

If A = {x : x is an even digit} and B = {x : x ≥ 0, x is integer} then
 
A ⊆ B   or   {0, 2, 4, 6, 8} ⊆ {0, 1, 2, 3, …}

 

Note: All sets under consideration belongs to a particular universal set.
 

Back to top

Complement of a Set

All set elements which belongs to U but do not belong to A is called the complement of set A and is denoted by Ac.
 

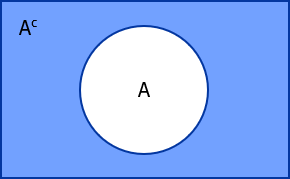
a-compliment.gif

 

Back to top

Disjoint Sets

Two sets are said to be disjoint if the sets contains no common element.
 

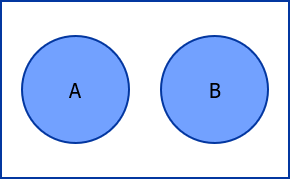
a-disjoint-b.gif

 

Back to top

Union

The union of two sets is the set of all elements which belongs to either or both sets.
 

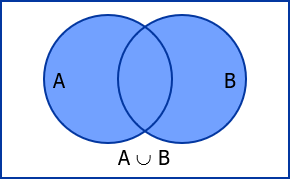
a-union-b.gif

 

The union of A and B is denoted by A ⋃ B.

$A \cup B = \{x : x \in A \text{ and/or } x \in B\}$

 

Example

If A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8} then A ⋃ B = {1, 2, 3, 4, 5, 6, 7, 8}

 

Back to top

Intersection

The intersection of two sets is the set of all elements which belongs to both sets.
 

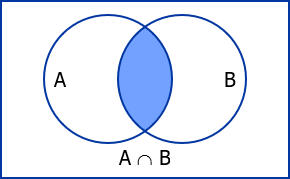
a-intersection-b.gif

 

The intersection of A and B is denoted by A ⋂ B.

$A \cap B = \{x : x \in A \text{ and } x \in B\}$

 

Example

If A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8} then A ⋂ B = {4, 5}

 

Note: If A and B are disjoint sets, then A ⋂ B = $\varnothing$.
 

Back to top

Difference

The difference of two sets, also called relative complement, is the set of elements which belongs to one set but do not belong to the other set.
 

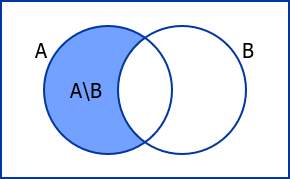
a-difference-b.gif

 

The difference of A and B is denoted by A\B.

$A \setminus B = \{x : x \in A \text{ and }, ~ x \notin B\}$

 

Example

If A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8} then A\B = {1, 2, 3}

 

Back to top

Symmetric Difference

The symmetric difference of two sets consists of those elements which belongs to either of the two sets but excludes the elements that belongs to both of the two.
 

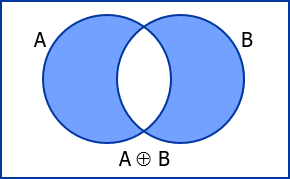
a-symmetric-difference-b.gif

 

The symmetric difference of A and B is denoted by A ⊕ B.

$A \oplus B = (A \cup B) \setminus (A \cap B)$   or   $A \oplus B = (A \setminus B) \cup (B \setminus A)$

 

Example

If A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8} then A ⊕ B = {1, 2, 3, 6, 7, 8}

 

Note: If A and B are disjoint sets, then A ⊕ B = A ⋃ B.
 

Back to top
Tags
Set Theory
Universal Set
Empty Set
Null Set
Subset
Element of a Set
Union
Intersection
Disjoint
Venn Diagrams
Set Complement