Plane Geometry

Back to top

Triangle

 

 

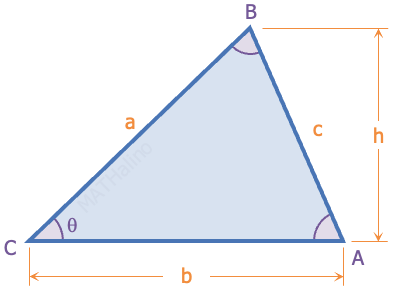
Perimeter, $P = a + b + c$

Semi-perimeter, $s = \frac{1}{2}P = \frac{1}{2}(a + b + c)$

Sum of included angles, $A + B + C = 180^\circ$

$\begin{align} \text{Area, } A & = \frac{1}{2} bh \\ & = \frac{1}{2}ab \sin \theta \\ & = \sqrt{s(s - a)(s - b)(s - c)} \end{align}$
 

Back to top

Quadrilateral

 

 

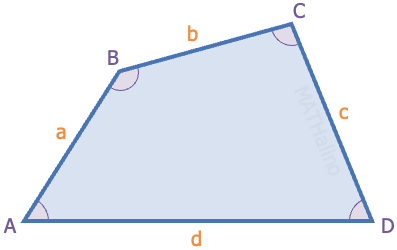
Perimeter, $P = a + b + c + d$

Semi-perimeter, $s = \frac{1}{2}P = \frac{1}{2}(a + b + c + d)$

Sum of included angles, $A + B + C + D = 360^\circ$
 

 

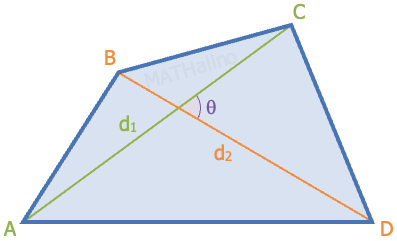
$\begin{align} \text{Area, } A & = \sqrt{(s - a)(s - b)(s - c)(s - d) - abcd \cos^2 \varphi} \\ & = \frac{1}{2} d_1 ~ d_2 \sin \theta \end{align}$

where, $\varphi = \frac{1}{2}(A + C)$ or $\varphi = \frac{1}{2}(B + D)$
 

Back to top

Regular Polygons

 

 

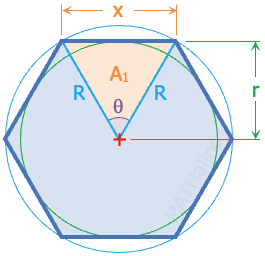
Perimeter, $P = nx$

Central angle of one segment, $\theta = \dfrac{360^\circ}{n}$

$\begin{align} \text{Area, } A & = nA_1 \\ & = \dfrac{n}{2} xr \\ & = \dfrac{n}{2} R^2 \sin \theta \end{align}$
 

Back to top

Circle

 

 

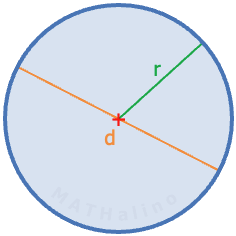
Circumference, $c = 2\pi r = \pi d$

$\begin{align} \text{Area, } A & = \pi r^2 \\ & = \dfrac{\pi}{4} d^2 \end{align}$