Solid Mensuration

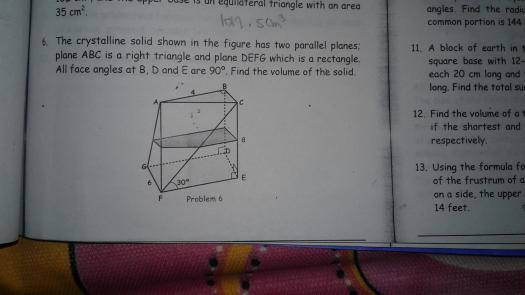
I'll just rewrite the question for others to search easily.

The crystalline solid shown in the figure below has two parallel planes; plane $ABC$ is a right triangle and plane $DEFG$ which is a rectangle. All face angles at $B$, $D$, and $E$ are $90^o$. Find the volume of the solid.

To solve the volume of the solid above, recall the formula of a prismatoid (The solid above is a prismatoid). The formula would be:

$$V = \frac{L}{6}(A_1 + 4A_{middle} + A_2)$$

where $V$ is the volume of the prismatoid, $L$ is the height of prismatoid, $A_2$ is the area at the bottom of the prismatoid, $A_{middle}$ is the area at the middle of the prismatoid, and $A_1$ is the area at the top of the prismatoid.

We notice we have the $L$ ($L = 8$) but we don't have the $A_1$, $A_{middle}$ and $A_2$. Now looking again at the figure and adding something noteworthy:

To get the $A_1$, it is pretty straightforward. Just get the area of triangle $A_1$.

$$A = \frac{1}{2}(base)(height)$$ $$A = \frac{1}{2}(6)(4)$$ $$A = 12 \space square \space units$$

To get the $A_{middle}$, it is pretty difficult. We need to find all the unknown lengths of the crystalline solid. The same goes in getting the $A_2$.

Now getting all the unknown lengths of the crystalline solid:

Let's get the length $\color{red}{a}$:

$$a^2 = 4^2 + 6^2$$ $$\color{red}{a = 7.2}$$

Let's get the length $\color{blue}{b}$:

$$\cos \theta = \frac{opposite}{hypotenuse}$$ $$\cos 30^o = \frac{8}{b}$$ $$\color{blue}{b = 16}$$

Let's get the length $\color{green}{c}$:

$$16^2 = c^2 + 8^2$$ $$\color{green}{c = 13.8}$$

Let's get the length $\color{yellow}{d}$

$$\tan \theta = \frac{opposite}{hypotenuse}$$ $$\tan 30^o = \frac{4}{d}$$ $$\color{yellow}{d = 6.9}$$

Let's get the length $\color{orange}{e}$:

$$e^2 = 6.9^2 + 4^2$$ $$e = 8$$

Let's get the length $\color{violet}{f}$

Very easy. Look at the figure. $$16-8 = \color{violet}{f = 8}$$

Let's get the length $\color{pink}{g}$:

Adding some details:

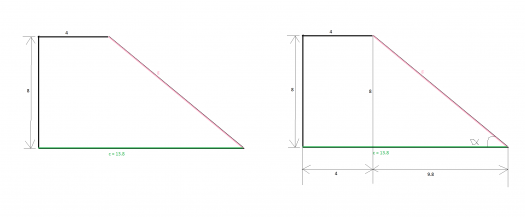
$$\tan \beta = \frac{8}{9.8}$$ $$\beta = 39.2^o$$

Now getting the length $\color{pink}{g}$...

$$g^2 = 8^2 + 9.8^2$$ $$\color{pink}{g = 12.6}$$

Now getting the length $\color{gray}{h}$:

Adding some details:

$$\tan 39.2^o = \frac{4}{x}$$ $$x = 4.9$$

And...

$$y = 13.8 - 4.9 = 8.9$$

Now getting the length $\color{gray}{h}$...

$$y = \color{gray}{h} = 8.9$$

Now getting the length $\color{brown}{i}$:

$$i^2 = 12.6^2 + 6^2$$ $$\color{brown}{i = 13.9}$$

Now getting the length $\color{gold}{j}$:

$$\tan \gamma = \frac{12.6}{6}$$ $$\gamma = 64.5^o$$

Now adding some details:

$$z^2 = 4^2 + 4.9^2$$ $$z = 6.3$$

Now getting the length $\color{gold}{j}$...

$$\tan \delta = \frac{j}{6.3}$$ $$\color{gold}{j = 3}$$

Now getting the length $\color{darkred}{k}$...

I'm tired...The value of length $\color{darkred}{k = 3.6}$. On how I got the value of $\color{darkred}{k = 3.6}$ is left for you as an exercise.

Now that we got all the unknown lengths, we can now get the areas $A_1$ and $A_{middle}$.

The area $A_2$ a rectangle, so the area would be:

$$Area_2 = (base)(height)$$ $$Area_2 = (6)(13.8)$$ $$Area_2 = 82.8 \space units^2$$

The area $A_{middle}$ is a composite of a trapezoid and a rectangle, so the area would be:

$$Area_{middle} = \frac{1}{2}h(b_1 + b_2) + (base)(height)$$ $$Area_{middle} = \frac{1}{2}(2)(6 + 3) + (6)(6.9)$$ $$Area_{middle} = 50.4 \space units^2$$

FINALLY!!!! the volume of the figure above is:

$$V = \frac{L}{6}(A_1 + 4A_{middle} + A_2)$$ $$V = \frac{8}{6}(12 \space units^2 + 4(50.4 \space units^2) + (82.8 \space units^2))$$ $$\color{green}{V = 395.2 \space cubic \space units}$$

In the book, the answer was $396.55 \space cubic \space units$. Pretty close to our answer.

Alternate solutions are encouraged:-)